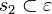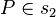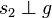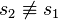Lösung Aufgabe 9.7 WS 12 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Bemerkung --*m.g.* 13:25, 26. Jan. 2013 (CET)) |
*m.g.* (Diskussion | Beiträge) (→Behauptung 2) |
||
| (19 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 7: | Zeile 7: | ||
Beweisen Sie:<br /> | Beweisen Sie:<br /> | ||
#<math>\exist s \subset \varepsilon: P \in s \wedge s \perp g </math> | #<math>\exist s \subset \varepsilon: P \in s \wedge s \perp g </math> | ||
| − | #<math>s_1 \subset \varepsilon \wedge P \in s_1 \wedge s \perp g \Rightarrow \neg \exist s_2: s_2 \subset \varepsilon \wedge P \in s_2 \wedge s_2 \perp g \wedge s_2 \not \equiv s_1 </math> | + | #<math>s_1 \subset \varepsilon \wedge P \in s_1 \wedge s \perp g \Rightarrow \neg \exist s_2: s_2 \subset \varepsilon \wedge P \in s_2 \wedge s_2 \perp g \wedge s_2 \not \equiv s_1 </math><br /><br /> |
| + | Tippfehler: | ||
| + | <math>s_1 \subset \varepsilon \wedge P \in s_1 \wedge s_1 \perp g \Rightarrow \neg \exist s_2: s_2 \subset \varepsilon \wedge P \in s_2 \wedge s_2 \perp g \wedge s_2 \not \equiv s_1 </math><br /> | ||
==Lösung von User ...== | ==Lösung von User ...== | ||
| Zeile 20: | Zeile 22: | ||
In der Ebene <math>\varepsilon</math> seien eine Gerade <math>g</math> und ein Punkt <math>P</math> mit <math>P \in g</math> gegeben.<br /> | In der Ebene <math>\varepsilon</math> seien eine Gerade <math>g</math> und ein Punkt <math>P</math> mit <math>P \in g</math> gegeben.<br /> | ||
Wir gehen also von einer Ebene <math>\varepsilon</math> aus. Ob die Existiert schert uns wenig. In <math>\varepsilon</math> möge eine Gerade <math>g</math> gelegen sein und auf dieser Geraden ein Punkt <math>P</math>. Sollte eine derartige Konstellation vorliegen, wissen wir Folgendes:<br /> | Wir gehen also von einer Ebene <math>\varepsilon</math> aus. Ob die Existiert schert uns wenig. In <math>\varepsilon</math> möge eine Gerade <math>g</math> gelegen sein und auf dieser Geraden ein Punkt <math>P</math>. Sollte eine derartige Konstellation vorliegen, wissen wir Folgendes:<br /> | ||
| − | + | =====Behauptung 1===== | |
| + | *<math>\exist s \subset \varepsilon: P \in s \wedge s \perp g </math><br /> | ||
Wir übersetzen: | Wir übersetzen: | ||
| Zeile 28: | Zeile 31: | ||
| <math>\exist s </math> || Es existiert eine Gerade <math>s</math>, | | <math>\exist s </math> || Es existiert eine Gerade <math>s</math>, | ||
|- | |- | ||
| − | | \subset \varepsilon|| die zu der Ebene <math>\varepsilon</math> gehört | + | | <math>\subset \varepsilon</math>|| die zu der Ebene <math>\varepsilon</math> gehört |
|- | |- | ||
| : ||und die folgenden Eigenschaften hat:, | | : ||und die folgenden Eigenschaften hat:, | ||
| + | |- | ||
| + | |<math>P \in s </math>|| der Punkt <math>P</math> gehört zu <math>s</math> bzw. anders ausgedrückt <math>s</math> geht durch <math>P</math> | ||
| + | |- | ||
| + | |<math>\wedge</math>|| und | ||
| + | |- | ||
| + | |<math>s \perp g </math>|| <math>s</math> steht senkrecht auf <math>g</math> | ||
|} | |} | ||
| − | *<math>\exist | + | Noch mal neu: |
| + | ::Zu jeder Geraden <math>p</math> und jedem Punkt <math>P</math> auf dieser Geraden <math>g</math> gibt es in jeder Ebene, die <math>g</math> enthält eine zu <math>g</math> senkrechte Gerade <math>s</math>, die durch <math>P</math> geht.<br /> | ||
| + | Oder: | ||
| + | ::In jeder Ebene, die eine Gerade enthält, gibt es in jedem Punkt dieser Geraden eine Senkrechte zu der Geraden. | ||
| + | =====Behauptung 2===== | ||
| + | *<math>s_1 \subset \varepsilon \wedge P \in s_1 \wedge s_1 \perp g \Rightarrow \neg \exist s_2: s_2 \subset \varepsilon \wedge P \in s_2 \wedge s_2 \perp g \wedge s_2 \not \equiv s_1 </math><br /> | ||
| + | |||
| + | Wir sehen den Implikationspfeil und setzen vor alles, was vor dem Pfeil steht ein ''Wenn'':<br /> | ||
| + | |||
| + | '''Wenn'''<br /> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | !Mathe!!Deutsch | ||
| + | |- | ||
| + | | <math>s_1 \subset \varepsilon</math> || die Gerade <math>s_1</math> zur Ebene <math>\varepsilon</math> gehört | ||
| + | |- | ||
| + | |<math>\wedge</math> || und | ||
| + | |- | ||
| + | | <math> P \in s_1</math> || durch den Punkt <math>P</math> geht | ||
| + | |- | ||
| + | | <math>\wedge</math> || und | ||
| + | |- | ||
| + | | <math>s_1 \perp g</math> || senkrecht auf <math>g</math> steht | ||
| + | |} | ||
| + | <br /> | ||
| + | Jetzt kommt der Implikationspfeil <math>\Rightarrow</math><br /> | ||
| + | Wir übersetzen ihn mit <br /><br /> | ||
| + | '''Dann''':<br /> | ||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | !Mathe!!Deutsch | ||
| + | |- | ||
| + | | <math>\neg \exist s_2</math> || existiert keine Gerade <math>s_2</math>, | ||
| + | |- | ||
| + | | <math>:</math> || die die folgenden Eigenschaften hat: | ||
| + | |- | ||
| + | | <math>s_2 \subset \varepsilon</math> || sie gehört (auch) zur Ebene <math>\varepsilon</math> | ||
| + | |- | ||
| + | | <math>\wedge</math> || und | ||
| + | |- | ||
| + | | <math>P \in s_2</math> || geht (auch) durch den Punkt <math>P</math> | ||
| + | |- | ||
| + | | <math>\wedge</math> || und | ||
| + | |- | ||
| + | | <math>s_2 \perp g</math> || steht (auch) senkrecht auf <math>g</math> | ||
| + | |- | ||
| + | | <math>\wedge</math> || und | ||
| + | |- | ||
| + | | <math>s_2 \not \equiv s_1</math> || sie ist von der Geraden <math>s_1</math> verschieden. | ||
| + | |||
| + | |} | ||
| + | |||
| + | Kurzübersetzung:<br /> | ||
| + | '''Es kann nur eine geben.'''<br /><br /> | ||
| + | '''Hinweis:''' Sie sollten für die Klausur in der Lage sein, sowas in angemessener Zeit korrekt zu übersetzen. | ||
| + | --[[Benutzer:*m.g.*|*m.g.*]] 14:23, 26. Jan. 2013 (CET)<br /> | ||
| + | Bezug zur Schule:<br /> | ||
| + | Das Ganze entspricht in gewisser Weise dem Erkennen und Übersetzen der Struktur von Termen in den Klassen 8 aufwärts. | ||
==Lösung von User ...== | ==Lösung von User ...== | ||
Aktuelle Version vom 26. Januar 2013, 15:24 Uhr
Aufgabe 9.7In der Ebene Tippfehler:
Lösung von User ...Lautet die Voraussetzung: Existenz ebene und g Element der ebene und p Element g Lautet die Behauptung : P Element s und s orthogonal zu g --Hauleri 14:36, 25. Jan. 2013 (CET) Bemerkung --*m.g.* 13:25, 26. Jan. 2013 (CET)Das steht so nirgends: Behauptung 1Wir übersetzen:
Noch mal neu:
Oder:
Behauptung 2Wir sehen den Implikationspfeil und setzen vor alles, was vor dem Pfeil steht ein Wenn: Wenn
Kurzübersetzung: Lösung von User ... |
 seien eine Gerade
seien eine Gerade  und ein Punkt
und ein Punkt  mit
mit 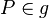 gegeben.
gegeben.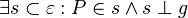
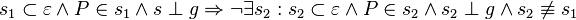
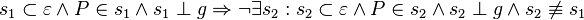
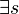
 ,
,
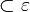
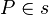

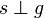
 und jedem Punkt
und jedem Punkt 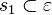
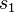 zur Ebene
zur Ebene 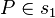
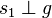

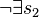
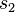 ,
,