Lösung der Aufgaben zur Mengenlehre (SoSe 12)

Mengenlehre

Aufgabe 1

A und B sind identisch. --PippiLotta 09:22, 18. Apr. 2012 (CEST)

Ich würde sagen B ist Teilmenge von A, da A mehr Zahlen besitzt als B. z.B besitzt B die Zahlen 1,2,3,5 .... nicht. Somit ist B Teilmenge von A.--Maliglowka 16:36, 18. Apr. 2012 (CEST)

Die Menge A besitzt die Zahlen 1,3 und 5 auch nicht, weil sie nur gerade natürliche Zahlen besitzt. Deswegen würde ich auch sagen, dass die Mengen identisch sind.
Freut mich, dass hier schon diskutiert wird. Ich fände es gut, wenn jeder seinen Kommentar signieren würde, damit man besser erkennen kann, welcher Kommentar von wem ist.--Tutor Andreas 17:02, 18. Apr. 2012 (CEST)

@Tutor Andreas: habs überlesen aber die Menge A hat ja gerade natürliche Zahlen und da zählt schon die 2 bzw beginnt bei der 2. Die erste natürliche Quadratzahl ist aber 4, somit enthält A alle Zahlen von B, aber B hat nicht die 2. Oder sehe ich da was falsches? --Maliglowka 23:38, 18. Apr. 2012 (CEST)
Der Vorschlag kam nicht von mir. Deshalb fände ich das mit den Signaturen auch gut... An dieser Aufgabe sieht man schon, wie sehr man auf Formulierungen und genaues Lesen achten muss. Hier noch einmal die Aufgabe, damit es vielleicht deutlicher wird.
Es sei A die Menge der geraden natürlichen Zahlen, B die Menge der natürlichen Zahlen, deren Quadrate gerade sind.
Die 2 gehört demnach zur Menga A, da die 2 gerade ist und die 2 gehört auch zur Menge B, da das Quadrat der 2, also 4, auch gerade ist. Ich hoffe, dass dir das weiterhilft.--Tutor Andreas 08:49, 19. Apr. 2012 (CEST)

Die Menge B besitzt aber die natürlichen Zahlen, deren Quadrate gerade sind. Da gehört die 2 auch dazu.. Also sind sie identisch. --Klärchen 08:36, 19. Apr. 2012 (CEST) Danke sehr :) hat geholfen ^^ --Maliglowka 9:33, 19. Apr. 2012 (CEST)

Hier habe ich mir mal eine alternative Lösung überlegt : A { n e N | Em e N : 2m = n } B { n e N | Em e N : (2m)² = n²} => A = B --Bischoffp 13:19, 20. Apr. 2012 (CEST)

ich habe über deine deine alternative lösung nachgedacht:
A sei die menge der geraden natürlichen zahlen: $\ A = \{n\in \mathbb{N} |\exist m\in \mathbb{N}.2m=n\}$
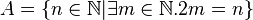
ich hätte für B ne andere lösung:
B sei die menge der natürlichen zahlen, deren quadrate gerade sind: $\ B= \{n\in\mathbb{N}| \exist p\in \mathbb{N}. n^2=2p\}$
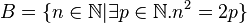
ausserdem glaube ich, dass wir nicht einfach A=B schreiben können.
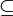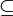um zu zeigen, dass A=B, müssten wir zeigen, dass A $\subseteq$ B $\wedge$ B$\subseteq$A,
dass also ein beliebiges n, das element von A ist, auch element aus B sein muss.
und dass jedes beliebige n, dass element aus B ist, auch element aus A sein muss,
oder? --Studentin 01:40, 21. Apr. 2012 (CEST)

Wenn du für deine Menge B z.B. p=3 setzt, dann wäre n meiner Meinung nach keine natürliche Zahl mehr. Wie ich die Äquivalenz hätte anders zeigen sollen , wusste ich nicht :)--Bischoffp 13:16, 21. Apr. 2012 (CEST)


ich will aber gar nicht p=3 setzen, sondern sage, dass in der menge b die zahlen n (aus den natürlichen zahlen) sind, deren quadratzahl gerade sind.
zu deren quadratzahlen also ein p (aus den natürlichen zahlen) existiert, bei dem gilt: n²=2p.
so gehört die 1 nicht zu der menge b: 1²=1 und es gibt kein p aus den natürlichen zahlen, so dass 2p=1
die zahl 2 gehört dazu: 2²=4, das dazu passende p=2
3 dagegen ist nicht element der menge: 3²=9 - dazu existiert kein passendes p
zu 4 dagegen existiert wieder ein p: die quadratzahl zu 4 ist 16, das existierende p lautet 8.
es ist nicht gefordert, dass es zu jedem p aus den natürlichen zahlen ein n geben muss (wie bei deinem bsp. mit der drei), du musst nur ein existierendes p finden, mit der das geforderte wahr wird.
lg--Studentin 21:37, 21. Apr. 2012 (CEST)

Aufgabe 2

M1={}
M2={}
M3={-2}
M4={}
M5= {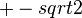$\ + - sqrt{2}$}
M6={-2}

M1=M2=M4
M3=M6--PippiLotta 09:22, 18. Apr. 2012 (CEST)

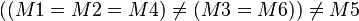$((M1=M2=M4)\neq (M3=M6))\neq M5$--Maliglowka 16:36, 18. Apr. 2012 (CEST)

Aufgabe 3

M1=M3 und M2 ist Teilmenge von M1/M3
Das stimmt leider nicht. Hier eine kleine Hilfe.--Tutor Andreas 14:10, 19. Apr. 2012 (CEST)

--Tutor Andreas 09:21, 19. Apr. 2012 (CEST)


--Studentin 16:47, 20. Apr. 2012 (CEST)
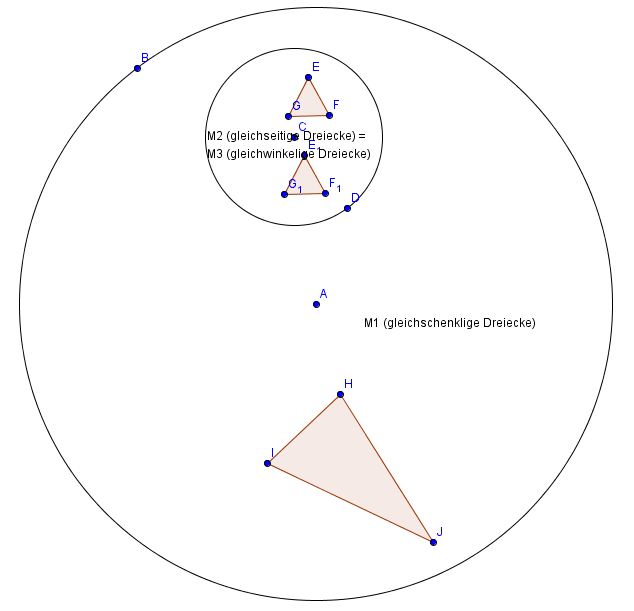
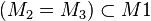$(M_2=M_3)\subset M1$ Und wie zeichnet man denn da bitteschön ein Venn-Diagramm mit Kreisen oder reicht es völlig aus wenn man es so wie du macht und so symbolisiert? --Maliglowka 9:37, 19. Apr. 2012 (CEST)
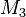Man muss die verschiedenen Mengen als Kreise darstellen. Da $M_2$ und $M_3$ die gleiche Klasse darstellen, sind sie im Venn-Diagramm auch nur als ein Kreis zu kennzeichnen. Dann muss man noch deutlich machen, dass 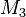$M_2$ ($M_3$) Teilmenge von 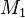$M_1$ ist. Vielleicht könnte jemand mit Geogebra eine Skizze entwerfen oder es als Bild hochladen...--Tutor Andreas 14:10, 19. Apr. 2012 (CEST)

Dazu hab ich nochmal ne Frage. Ich hab es auch wie Studentin. Wir sollten es ja als Venn-Diagramm darstellen, aber wenn ich es schreiben würde, kann ich das dann auch so machen? 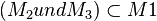$(M_2 und M_3)\subset M1$ Das "und"-Zeichen konnte ich nicht finden, aber eigentlich sollte das da hin... --Nala23 13:02, 22. Apr. 2012 (CEST)

Aufgabe 4

N1=N2=N3, alles Rechtecke

Wurzelzeichen? Hier ist eins: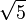$\sqrt{5}$ (Quelltext anschauen) Ansonsten in der Hilfe nachsehen: Formeln_verwenden--*m.g.* 17:17, 18. Apr. 2012 (CEST)

Schöne Diskussionen und so sind die Aufgaben gemeinsam richtig gelöst!--Tutorin Anne 16:45, 19. Apr. 2012 (CEST)