Lösung von Aufg. 12.8 SS11
Es seien  ein Quadrat und
ein Quadrat und  eine positive reelle Zahl, die kleiner als die Seitenlänge von
eine positive reelle Zahl, die kleiner als die Seitenlänge von  ist. Ferner seien die Punkte
ist. Ferner seien die Punkte 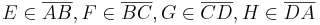 mit
mit 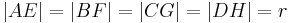 gegeben. Man beweise:
gegeben. Man beweise: 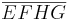 ist ein Quadrat.
ist ein Quadrat.
Was ist ein Quadrat ?--Peterpummel 18:24, 3. Jul. 2011 (CEST)
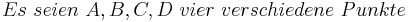
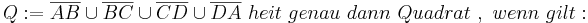
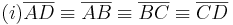
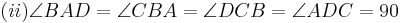
Eine Skizze von der Aufgabe hilft enorm
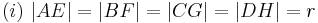
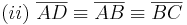
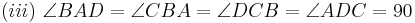
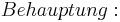
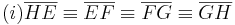
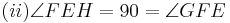
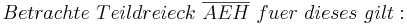
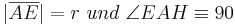
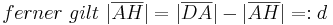
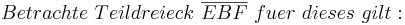
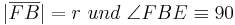
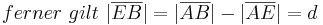
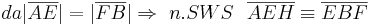

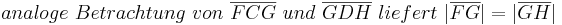
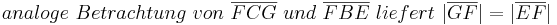
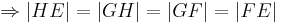
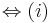
Aus unserer Übung mit dem Parallelaxiom gehe ich nun von dessen Gültigkeit aus und benutze nun den Innenwinkelsummensatz vom Dreieck. Ansonsten sehe ich keine Möglichkeit die rechten Winkel im Quadrat nachzuweisen
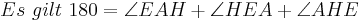
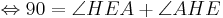
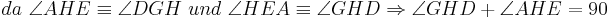
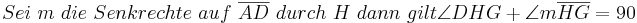
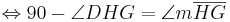
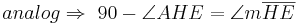
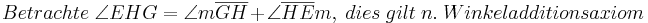
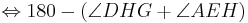
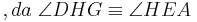
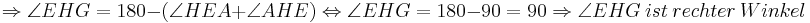
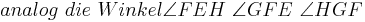
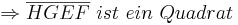
bei den Rechnungen mit den Winkeln stehen keine Betragsstriche dabei, korrekter Weise müssten sie gesetzt werden. Ich bitte das zu beachten.
Vielleicht findet ja jemand eine kürzere und schönere Lösung. Die Definition des Quadrats macht mir den Beweis etwas umständlich, vielleicht einen schönere Definition vom Quadrat anbieten.
--Peterpummel 15:41, 4. Jul. 2011 (CEST)

