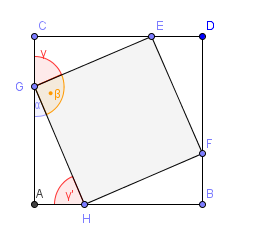
Lösung von Aufg. 12.8 SS11
Es seien  ein Quadrat und
ein Quadrat und  eine positive reelle Zahl, die kleiner als die Seitenlänge von
eine positive reelle Zahl, die kleiner als die Seitenlänge von  ist. Ferner seien die Punkte
ist. Ferner seien die Punkte 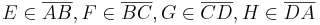 mit
mit 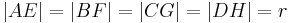 gegeben. Man beweise:
gegeben. Man beweise: 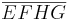 ist ein Quadrat.
ist ein Quadrat.
Was ist ein Quadrat ?--Peterpummel 18:24, 3. Jul. 2011 (CEST)
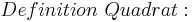
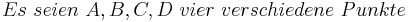
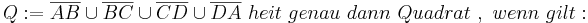
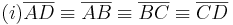
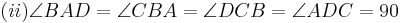
Damit ist eine überbestückte Definition. Alle Eigenschaften treffen zwar auf ein Quadrat zu, doch sollte eine formale Definition nur wirklich nötige Eigenschaften enthalten, damit der Begriff ausreichend klar ist.--Tutorin Anne 18:11, 5. Jul. 2011 (CEST)
Eine Skizze von der Aufgabe hilft enorm
Ja, erstellen Sie doch (das nächste Mal) eine einfache Skizze in Geogebra selbst :).
Ich dachte da ich schon den ganzen Text in Latex der Übersicht zu liebe geschrieben habe darf sich ein anderer an einer Skizze versuchen;)--Peterpummel 14:20, 6. Jul. 2011 (CEST)
--Tutorin Anne 18:11, 5. Jul. 2011 (CEST)
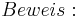
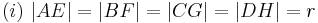
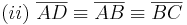
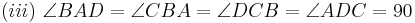
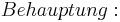
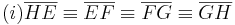
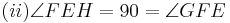
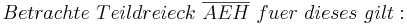
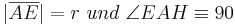
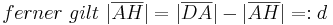
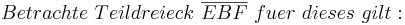
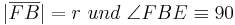
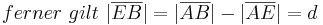
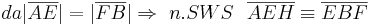

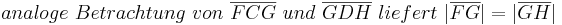
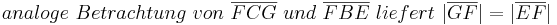
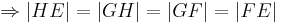
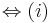
Aus unserer Übung mit dem Parallelaxiom gehe ich nun von dessen Gültigkeit aus und benutze nun den Innenwinkelsummensatz vom Dreieck. Ansonsten sehe ich keine Möglichkeit die rechten Winkel im Quadrat nachzuweisen
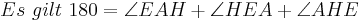
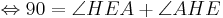
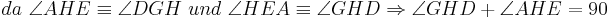
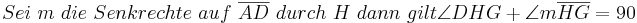
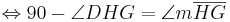
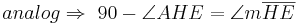
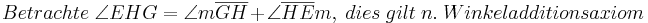
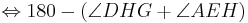
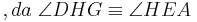
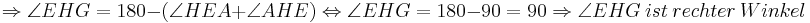
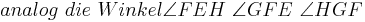
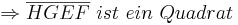
bei den Rechnungen mit den Winkeln stehen keine Betragsstriche dabei, korrekter Weise müssten sie gesetzt werden. Ich bitte das zu beachten.
Vielleicht findet ja jemand eine kürzere und schönere Lösung. Die Definition des Quadrats macht mir den Beweis etwas umständlich, vielleicht einen schönere Definition vom Quadrat anbieten.
--Peterpummel 15:41, 4. Jul. 2011 (CEST)
Danke fürs Reinstellen! Dein Beweis ist sehr ausführlich. Die Beweisidee ist völlig korrekt, bestimmt lässt sich der Beweis (vorallem der 2.Teil) auch kürzer aufschreiben. Mit den Winkelbezeichnungen ist er etwas schwirig nachzuvollziehen. Das nächste Mal lieber eine Skizze machen (Scannen oder Paint geht ja auch!) und die Winkel konkret benennen.--Tutorin Anne 18:28, 5. Jul. 2011 (CEST)
Ich denke, es genügt, nach dem Nachweis der Dreieckskongruenz auf die kongruenten Winkel Gamma und Gamma-Strich hinzuweisen
und dann über die Winkeladdition sowie die Größe des gestreckten Winkels insgesamt darauf zu kommen, dass die Größe von Beta 90 Grad betragen muss. Und ein einziger rechter Winkel im Quadrat reicht ja bei vier gleich langen Seiten.
Würde das als kürzerer zweiter Schritt gehen? --WikiNutzer 15:43, 7. Jul. 2011 (CEST)
Richtig, es genügt, wenn man für einen Winkel des Quadrats die 90° zeigt. Dabei ist es sinnvoll, die genauen Additionen der Winkelmaße aufzuschreiben und mit den jeweiligen Sätzen und Axiomen zu begründen, z.B. tabelarisch. --Tutorin Anne 16:38, 8. Jul. 2011 (CEST)
Man kann doch auch zeigen, dass alle Teildreiecke gleich groß sind, somit die Seiten des Quadrats gleich sind
und somit auch, dass alle fehlenden Supplementwinkel (also die Winkel des Quadrats) gleich groß sind.
Und dann ergibt sich ja aus 360:4, dass jeder Winkel 90 ist.
Würde das auch gehen? Das ging eigentlich ganz schnell.--mm_l 10:54, 15. Jul. 2011 (CEST)
Die Beweisidee ist richtig.
Achte auf deine Ausdrucksweise: Was sind gleichgroße Teildreicke? Gleicher Flächeninhalt? So hört es sich an, obwohl du vermutlich zueinander kongruente Dreicke meinst.--Tutorin Anne 10:48, 17. Jul. 2011 (CEST)