Lösung von Aufg. 9.4 (WS 11/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Gegeben seien drei paarweise verschiedene und '''kollineare''' Punkte ''A'', ''B'' und ''C'' in einer Ebene ''E''. Ferner sei eine Gerade ''g'' Teilmenge der Eben…“) |
RicRic (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
Gegeben seien drei paarweise verschiedene und '''kollineare''' Punkte ''A'', ''B'' und ''C'' in einer Ebene ''E''. Ferner sei eine Gerade ''g'' Teilmenge der Ebene ''E'', wobei keiner der Punkte ''A'', ''B'' und ''C'' auf ''g'' liegen möge. Beweisen Sie folgenden Zusammenhang:<br /><br /> | Gegeben seien drei paarweise verschiedene und '''kollineare''' Punkte ''A'', ''B'' und ''C'' in einer Ebene ''E''. Ferner sei eine Gerade ''g'' Teilmenge der Ebene ''E'', wobei keiner der Punkte ''A'', ''B'' und ''C'' auf ''g'' liegen möge. Beweisen Sie folgenden Zusammenhang:<br /><br /> | ||
<math>\overline{AB} \cap g \neq \lbrace \rbrace \wedge \overline{BC} \cap g = \lbrace \rbrace \Rightarrow \overline{AC} \cap g \neq \lbrace \rbrace </math> <br /> | <math>\overline{AB} \cap g \neq \lbrace \rbrace \wedge \overline{BC} \cap g = \lbrace \rbrace \Rightarrow \overline{AC} \cap g \neq \lbrace \rbrace </math> <br /> | ||
| + | <br /><br /> | ||
| + | Vor.: <math>\operatorname{koll}(A, B, C) \wedge A\neq B\neq C\neq D \wedge A,B,C\in E</math><br /> | ||
| + | Beh.: <math>\overline{AB} \cap g \neq \lbrace \rbrace \wedge \overline{BC} \cap g = \lbrace \rbrace \Rightarrow \overline{AC} \cap g \neq \lbrace \rbrace </math> <br /> | ||
| + | Beweis:<br /> | ||
| − | + | {| class="wikitable sortable" | |
| + | !Schritt!!Begründung | ||
| + | |- | ||
| + | | (1)<math>\operatorname{koll}(A, B, C)</math> || Vorr | ||
| + | |- | ||
| + | | (2)<math>\operatorname(Zw) (A, B, C) entweder oder \operatorname(Zw) (B, C, A) entweder oder \operatorname(Zw) (C, A, B)</math> || Dreiecksungleichung, Abstand kann nicht negativ sein | ||
| + | |- | ||
| + | | (3)Fall 1: <math>\operatorname(Zw) (A, B, C)</math> <br /><math>\ g \cap \overline{AB} =\left\{ {S} \right\} \Rightarrow \ g \cap \overline{AB}=\phi</math><br /><math>\overline{AB} c\overline{AC}</math> <br /><math>\ g \cap \overline{AC} =\left\{ {S} \right\}</math> Behaupt stimmt || verschiedene Geraden haben höchstens einen Punkt gemeinsam, zw Relation, Teilmengenbezieung | ||
| + | |- | ||
| + | | Fall 2: <math>\operatorname(Zw) (B, C, A)</math> <br /><math>\ g \cap \overline{AB} =\left\{ {S} \right\} \Rightarrow \ entweder: g \cap \overline{BC}=\left\{ {S} \right\} oder g \cap \overline{BC}=\left\{ {S} \right\}</math> <br /> Wiederspruch zur Behauptung | ||
| + | |- | ||
| + | | Fall 3: <math>\operatorname(Zw) (A, B, C)</math> <br /><math>\ g \cap \overline{AB} =\left\{ {S} \right\} \Rightarrow entweder: g \cap \overline{BC}=\left\{ {S} \right\} \wedge g \cap \overline{AC}=\phi</math> oder: g \cap \overline{AC}=\left\{ {S} \right\} \wedge g \cap \overline{BC}=\phi</math> | ||
| + | |- | ||
| + | | (4)<math>\exists P : P \operatorname{nkoll}(A, B, C)</math> || A I/3 | ||
| + | |- | ||
| + | | (5) <math>\overline{ABP}</math> || AI/1 | ||
| + | |- | ||
| + | | (6) <math>\overline{BCP}</math> || AI/1 | ||
| + | |- | ||
| + | | (7) <math>\overline{ACP}</math> || AI/1 | ||
| + | |- | ||
| + | | (8) Fall 1: <math>P\in g</math>betrachte ich nachher<br /><math>P\notin g</math> || | ||
| + | |- | ||
| + | | (9) <math>\ g \cap \overline{AB}= \left\{ {S} \right\} \Rightarrow entweder: \ g \cap \overline{AP}= \left\{ {H}\right\} oder:\ g \cap \overline{BP}= \left\{ {H} \right\}</math> || Axiom von Pasch ,(5) | ||
| + | |- | ||
| + | | (10) <math>\ g \cap \overline{BC} =\phi \Rightarrow entweder:g \cap \overline{BP} =\phi \wedge g \cap \overline{CP} =\phi oder: <math>\ g \cap \overline{BP}= \left\{ {S} \right\} \wedge <math>\ g \cap \overline{CP}= \left\{ {H} \right\}</math> || Axiom von Pasch ,(6) | ||
| + | |- | ||
| + | | (11) <math>\ g \cap \overline{AC}= \left\{ {S} \right\} \Rightarrow entwerder: \ g \cap \overline{CP}= \left\{ {H} \right\} oder: \ g \cap \overline{AP}= \left\{ {H} \right\}</math> || Axiom von Pasch ,(7) | ||
| + | |- | ||
| + | | (12) <math>\left| AB \right| +\left| BC \right| =\left| AC \right|</math> || (3) | ||
| + | |- | ||
| + | | (13) <math>\overline{AB} c\overline{AC}</math> || (12) | ||
| + | |- | ||
| + | | (14) <math>\ g \cap \overline{AB} =\left\{ {S} \right\} \Rightarrow \ g \cap \overline{AC} =\left\{ {S} \right\}</math> || (9),10),(11),(13) | ||
| + | |- | ||
| + | | Fall 2 von (7) analog nur mit <math>\overline{AP} \in g</math> | ||
| + | |}Ich denke es sind noch einige Fehler drin, traue mich dennoch mal :-)--[[Benutzer:RicRic|RicRic]] 23:15, 8. Dez. 2011 (CET) | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 9. Dezember 2011, 00:15 Uhr
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
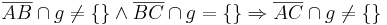
Vor.: 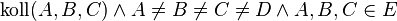
Beh.: 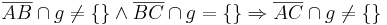
Beweis:
| Schritt | Begründung |
|---|---|
(1)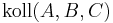 |
Vorr |
(2)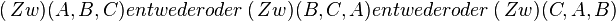 |
Dreiecksungleichung, Abstand kann nicht negativ sein |
(3)Fall 1: 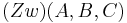 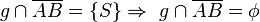 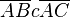 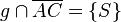 Behaupt stimmt Behaupt stimmt |
verschiedene Geraden haben höchstens einen Punkt gemeinsam, zw Relation, Teilmengenbezieung |
Fall 2: 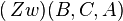 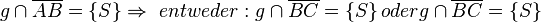 Wiederspruch zur Behauptung | |
Fall 3: 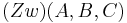 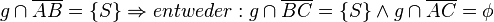 oder: g \cap \overline{AC}=\left\{ {S} \right\} \wedge g \cap \overline{BC}=\phi</math> oder: g \cap \overline{AC}=\left\{ {S} \right\} \wedge g \cap \overline{BC}=\phi</math>
| |
(4)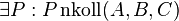 |
A I/3 |
(5) 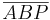 |
AI/1 |
(6) 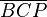 |
AI/1 |
(7) 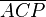 |
AI/1 |
(8) Fall 1: 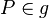 betrachte ich nachher betrachte ich nachher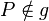 |
|
(9) 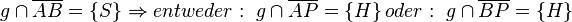 |
Axiom von Pasch ,(5) |
(10) 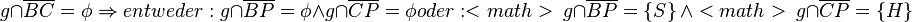 |
Axiom von Pasch ,(6) |
(11) 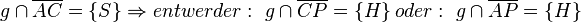 |
Axiom von Pasch ,(7) |
(12)  |
(3) |
(13) 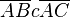 |
(12) |
(14) 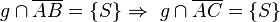 |
(9),10),(11),(13) |
Fall 2 von (7) analog nur mit 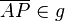
|

