Lösung von Aufgabe 10.5: Unterschied zwischen den Versionen
TimoRR (Diskussion | Beiträge) (→Beweis Versuch 1:) |
(→Beweis Versuch 1:) |
||
| Zeile 42: | Zeile 42: | ||
Das war ja jetzt der Beweis für die Existenz, fehlt jetzt noch einer für die Eindeutigkeit!? | Das war ja jetzt der Beweis für die Existenz, fehlt jetzt noch einer für die Eindeutigkeit!? | ||
Wenn ja, wie sähe der dann aus!? Reicht dafür das Winkelkonstruktionsaxiom!? --[[Benutzer:TimoRR|TimoRR]] 17:00, 6. Jul. 2010 (UTC) | Wenn ja, wie sähe der dann aus!? Reicht dafür das Winkelkonstruktionsaxiom!? --[[Benutzer:TimoRR|TimoRR]] 17:00, 6. Jul. 2010 (UTC) | ||
| + | |||
| + | Bei dem Satz wird nicht zwischen Existenz und Eindeutigkeit der Winkelhalbierenden unterschieden. Das kommt doch nur vor, wenn "genau" im Satz steht. Kann es sein dass du den Satz: "Jeder Winkel hat genau eine Winkelhalbierende" meinst? Da muss man dann nämlich Existenz und Eindeutigkeit beweisen. Hier ist nur gezeigt, dass bei einer Winkelhalbierenden (VSS) die Winkel, die durch die Winkelhalbierenden entstehen gleichgroß sind und diese das halbe Maß des Gesamtwinkel (Beh) haben. --[[Benutzer:Löwenzahn|Löwenzahn]] 17:56, 6. Jul. 2010 (UTC) | ||
Version vom 6. Juli 2010, 19:56 Uhr
Satz VI.1/2:
Es sei 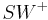 eine Winkelhalbierende des Winkels
eine Winkelhalbierende des Winkels  .
.
Dann gilt: 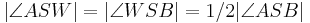
Beweis Versuch 1:
VSS: 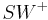 eine Winkelhalbierende des Winkels
eine Winkelhalbierende des Winkels 
Beh: 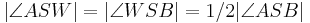
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 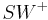 eine Winkelhalbierende von eine Winkelhalbierende von 
|
(VSS) |
| (II) | 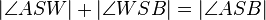
|
Winkeladditionsaxiom, W liegt im Innern von 
|
| (III) | 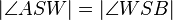
|
(I), Def. Winkelhalbierende |
| (IV) | 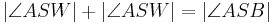
|
(II), (III), (rechnen mit reellen Zahlen) |
| (V) | 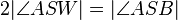 --> --> 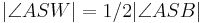
|
(IV), (rechnen mit reellen Zahlen) |
| (VI) | 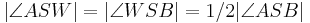
|
(III), (V) |
qed --Löwenzahn 17:51, 1. Jul. 2010 (UTC)
Das war ja jetzt der Beweis für die Existenz, fehlt jetzt noch einer für die Eindeutigkeit!? Wenn ja, wie sähe der dann aus!? Reicht dafür das Winkelkonstruktionsaxiom!? --TimoRR 17:00, 6. Jul. 2010 (UTC)
Bei dem Satz wird nicht zwischen Existenz und Eindeutigkeit der Winkelhalbierenden unterschieden. Das kommt doch nur vor, wenn "genau" im Satz steht. Kann es sein dass du den Satz: "Jeder Winkel hat genau eine Winkelhalbierende" meinst? Da muss man dann nämlich Existenz und Eindeutigkeit beweisen. Hier ist nur gezeigt, dass bei einer Winkelhalbierenden (VSS) die Winkel, die durch die Winkelhalbierenden entstehen gleichgroß sind und diese das halbe Maß des Gesamtwinkel (Beh) haben. --Löwenzahn 17:56, 6. Jul. 2010 (UTC)

