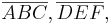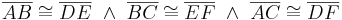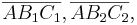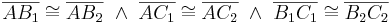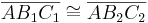Lösung von Aufgabe 11.3: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 69: | Zeile 69: | ||
:<math>\overline{AB_1C_1} \cong \overline{AB_2C_2}</math> | :<math>\overline{AB_1C_1} \cong \overline{AB_2C_2}</math> | ||
<br /> | <br /> | ||
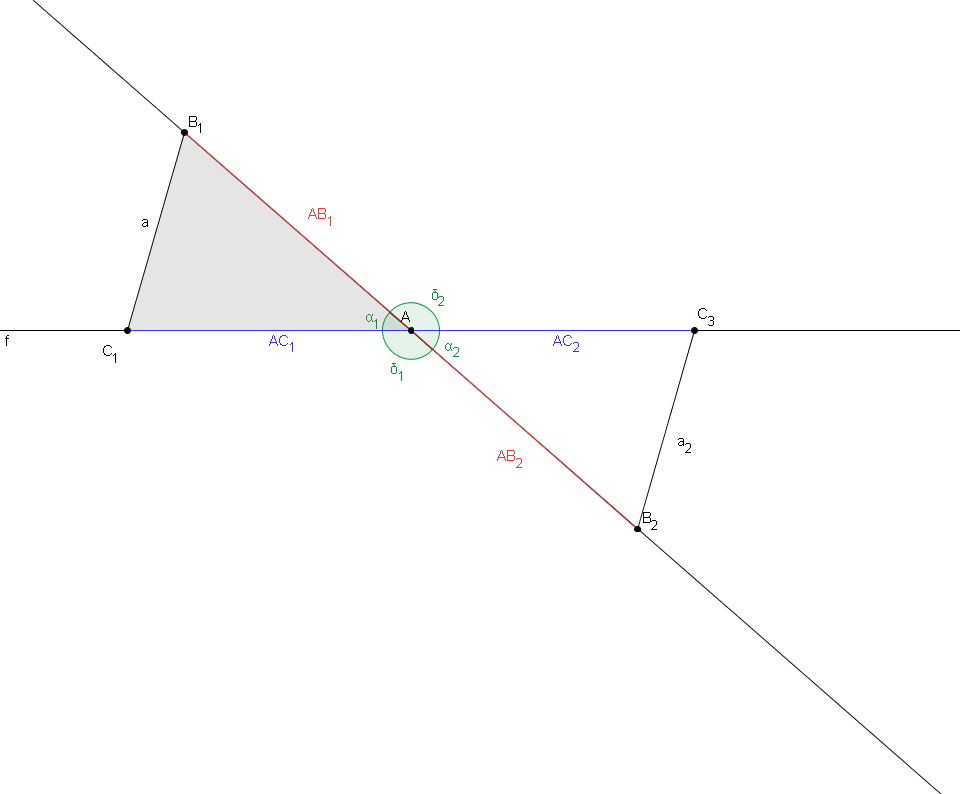
| − | [[Bild:Geo_Übung_11_3.png | + | [[Bild:Geo_Übung_11_3.png]]<br /> |
<br /> | <br /> | ||
| Zeile 77: | Zeile 77: | ||
| No. || Schritt || Begründung | | No. || Schritt || Begründung | ||
|- | |- | ||
| − | | 1 || Es existiert ein Punkt <math>C_2</math> für den gilt <math>\overline{AC_2} = \overline{AC_1},</math> ||Satz III.1: Jede Strecke hat einen und nur einen Mittelpunkt. <math> | + | | 1 || Es existiert ein Punkt <math>C_2</math> für den gilt <math>\overline{AC_2} = \overline{AC_1},</math> ||Satz III.1: Jede Strecke hat einen und nur einen Mittelpunkt. <math>A</math> ist Mittelpunkt der Strecke <math>\overline{C_1C_2}</math> |
Version vom 7. Juli 2010, 16:05 Uhr
Beweisen Sie den Kongruenzsatz SSS.
Lösung 1
Vor.:
Beh.:
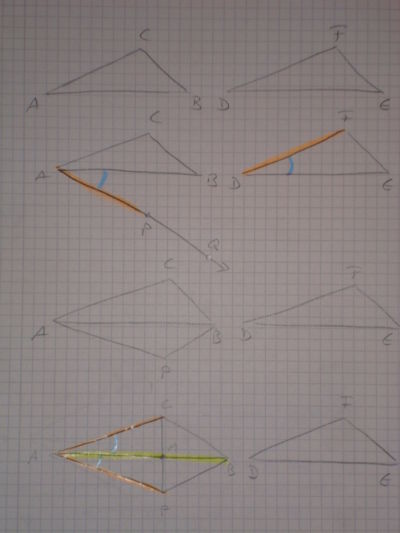
Bew.:
- Es ex. ein Strahl
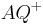 mit
mit 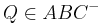 und
und  bzw.
bzw. 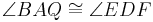 (Begr.: Winkelkonstruktionsaxiom).
(Begr.: Winkelkonstruktionsaxiom).
- Es ex. außerdem ein Punkt
 mit
mit 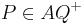 und
und  bzw.
bzw. 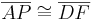 (Begr.: Axiom vom Lineal).
(Begr.: Axiom vom Lineal).
- Wir haben nun also ein Dreieck
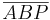 konstruiert, dass kongruent zu
konstruiert, dass kongruent zu  ist. Denn es gilt ja
ist. Denn es gilt ja 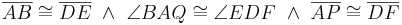 . Jetzt genügt es zu zeigen,
. Jetzt genügt es zu zeigen,  kongruent zu
kongruent zu 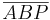 ist. Denn die Kongruenz ist transitiv, es würde daraus also auch
ist. Denn die Kongruenz ist transitiv, es würde daraus also auch 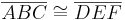 folgen.
folgen.
z.z.:
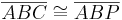
- Dafür wiederum genügt es nach dem Kongruenzaxiom sws zu zeigen, dass
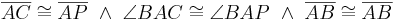 .
.
- Nach Vor. gilt
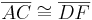 .
.
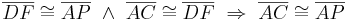 (Begr.: Transitivität, eigentlich fast trivial)
(Begr.: Transitivität, eigentlich fast trivial)
- Kongruenz ist reflexiv, also ist auch klar, dass
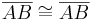 gilt.
gilt.
- Also bleibt nun noch
z.z.:
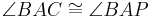
- Fürs weitere Vorgehen wieder eine kurze Feststellung, die eigentlich jeder sieht:
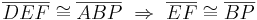
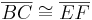 (Vor.)
(Vor.) 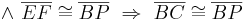
- Ich gehe davon aus, dass der folgende Satz gilt, ohne ihn jetzt zu beweisen:
- Satz: Liegt ein Punkt
 auf der Mittelsenkrechten
auf der Mittelsenkrechten  der Strecke
der Strecke  , dann und nur dann hat er von
, dann und nur dann hat er von  und
und  den gleichen Abstand.
den gleichen Abstand.
- Satz: Liegt ein Punkt
 hat ja nun den gleichen Abstand von
hat ja nun den gleichen Abstand von  wie von
wie von  , also
, also  .
.
- Für
 gilt Entsprechendes, also
gilt Entsprechendes, also  .
.
- Nach dem Satz liegen also
 und
und  auf der Mittelsenkrechten von
auf der Mittelsenkrechten von 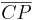 . Es ist sogar so, dass die Gerade
. Es ist sogar so, dass die Gerade  die Mittelsenkrechte von
die Mittelsenkrechte von 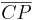 ist (Begr.: irgendein Inzidenzaxiom).
ist (Begr.: irgendein Inzidenzaxiom).
- Nach Def. der Mittelsenkrechten ist der Schnittpunkt
 von
von  und
und 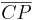 der Mittelpunkt von
der Mittelpunkt von 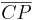 , d.h.
, d.h.  bzw.
bzw. 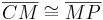 .
.
- Nach Def. gilt außerdem
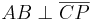 , d.h. die entstehenden Winkel sind rechte Winkel.
, d.h. die entstehenden Winkel sind rechte Winkel.
- Nun gilt nach Def. vom rechten Winkel, dass sie gleich groß sind bzw. damit auch kongruent, also
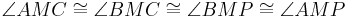 .
.
- Mit dieser Winkelkongruenz sind wir nur noch wenige Schritte vom Ziel entfernt.
- Wegen des Kongruenzaxioms sws wissen wir nun, dass die Dreiecke
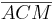 und
und 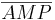 kongruent sind, denn es gilt:
kongruent sind, denn es gilt: 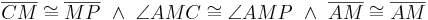 .
.
- Nach der Def. der Dreieckskongruenz sind dann auch die Winkel
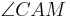 und
und 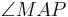 kongruent.
kongruent.
- Jetzt sieht es jeder, aber der Vollständigkeit halber sollte man noch zeigen, dass diese Winkel die gleichen sind wie die, die wir vorhin schon gemeint haben.
z.z.:
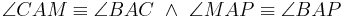
- Der Winkel
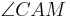 besteht aus den Schenkeln
besteht aus den Schenkeln 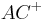 und
und 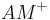 . Wir wissen aber, dass
. Wir wissen aber, dass  auf
auf  liegt. Also ist
liegt. Also ist 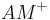 identisch mit
identisch mit 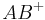 . Also auch
. Also auch 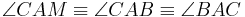 .
.
- Entsprechendes gilt für
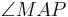 , also
, also 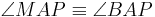 .
.
q.e.d.
Lösung 2
Vor.:
Beh.:
| No. | Schritt | Begründung |
| 1 | Es existiert ein Punkt 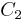 für den gilt für den gilt 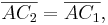 |
Satz III.1: Jede Strecke hat einen und nur einen Mittelpunkt.  ist Mittelpunkt der Strecke ist Mittelpunkt der Strecke 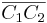
|
| 2 | Schritt | Begründung |