Lösung von Aufgabe 12.4: Unterschied zwischen den Versionen
| Zeile 8: | Zeile 8: | ||
<br />Hilfskonstruktion: Es existieren zwei VERSCHIEDENE Punkte <math>\ A \in g</math> und <math>\ B \in g</math> mit dem selben Abstand zu <math>\ P</math> | <br />Hilfskonstruktion: Es existieren zwei VERSCHIEDENE Punkte <math>\ A \in g</math> und <math>\ B \in g</math> mit dem selben Abstand zu <math>\ P</math> | ||
<br /><br />Kommentar --[[Benutzer:*m.g.*|*m.g.*]] 10:18, 13. Jul. 2010 (UTC): Begründen müssten Sie die Korrektheit der Hilfskonstruktion schon. Woher wissen Sie, dass die beiden Punkte <math>\ A</math> und <math>\ B</math> existieren? | <br /><br />Kommentar --[[Benutzer:*m.g.*|*m.g.*]] 10:18, 13. Jul. 2010 (UTC): Begründen müssten Sie die Korrektheit der Hilfskonstruktion schon. Woher wissen Sie, dass die beiden Punkte <math>\ A</math> und <math>\ B</math> existieren? | ||
| + | <br /> Re --[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 00:32, 15. Jul. 2010 (UTC): Beweis wurde nun weiter unten aufgeführt. Funktioniert das so? | ||
{| class="wikitable" | {| class="wikitable" | ||
! Nr. | ! Nr. | ||
| Zeile 23: | Zeile 24: | ||
! style="background: #FFDDDD;"|(III) | ! style="background: #FFDDDD;"|(III) | ||
| <math>\angle PAB \cong \angle PBA</math> | | <math>\angle PAB \cong \angle PBA</math> | ||
| − | | Gleichschenkliges Dreieck | + | | Gleichschenkliges Dreieck, Basiswinkelsatz |
|- | |- | ||
! style="background: #FFDDDD;"|(IV) | ! style="background: #FFDDDD;"|(IV) | ||
| Zeile 40: | Zeile 41: | ||
| (V), Definition rechte Winkel: kongruente Nebenwinkel | | (V), Definition rechte Winkel: kongruente Nebenwinkel | ||
|} | |} | ||
| − | <br />Es existiert ein Strahl <math>\ MP^+</math>, der mit <math>\ MA^+</math> oder <math>\ MB^+</math> einen rechten Winkel bildet, anders ausgedrückt: Es existiert eine Senkrechte auf <math>\ g</math> (da <math>\ A \in g</math> und <math>\ B \in g</math>), die durch <math>\ P</math> geht. | + | <br />Es existiert ein Strahl <math>\ MP^+</math>, der mit <math>\ MA^+</math> oder <math>\ MB^+</math> einen rechten Winkel bildet, anders ausgedrückt: Es existiert eine Senkrechte auf <math>\ g</math> (da <math>\ A \in g</math> und <math>\ B \in g</math> und <math>\ M \in g</math>), die durch <math>\ P</math> geht. |
| − | <br />zu Schritt (I): | + | <br />zu Schritt (I): Im weiteren Beweis wird klar, was man schon länger vermutete: dass ein Punkt <math>\ P</math> zu entweder keinem, zu einem oder zu zwei Punkten einer Gerade <math>\ g</math> einen bestimmten Abstand hat. Der Fall, dass wir eine Strecke von <math>\ P</math> auf dem Strahl <math>\ p</math> antragen und keinen Schnittpunkt mit <math>\ g</math> erhalten, kann man schnell ad acta legen, macht keinen Sinn! Wenn es nur einen Punkt gibt, dann sind wir fertig, das ist das Lot (das kann später bewiesen werden). |
| + | <br />Genau genommen ist der Schritt (1) also: Wir wählen einen beliebigen Punkt <math>\ A \in g</math> und tragen (nach Axiom vom Lineal) die Strecke <math>|\overline{PA}|</math> auf einem zweiten Strahl von <math>\ P</math> aus an und finden so den Punkt <math>\ B \in g</math>. | ||
| + | <br />Falls es keinen zweiten Punkt gibt, wählen wir von diesem Punkt <math>\ A \in g</math> eine beliebige Strecke, die wir "auf der Geraden <math>\ g</math>" abtragen und nun einen Punkt <math>\ A' \in g</math> bekommen und in der anderen Halbebene bzgl. <math>\ PA</math> einen weiteren Punkt mit dem selben Abstand. | ||
<br />--[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 00:27, 13. Jul. 2010 (UTC) | <br />--[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 00:27, 13. Jul. 2010 (UTC) | ||
| Zeile 63: | Zeile 66: | ||
#Es existiert ein zweiter Punkt <math>\ Q' \in g</math> mit dem Abstand <math>\ |PQ|</math> | #Es existiert ein zweiter Punkt <math>\ Q' \in g</math> mit dem Abstand <math>\ |PQ|</math> | ||
| Den Fall: "Es existiert kein Punkt..." haben wir in (I) und (II) ausgeschlossen. | | Den Fall: "Es existiert kein Punkt..." haben wir in (I) und (II) ausgeschlossen. | ||
| − | <br />Den Fall "Es existieren mehr als zwei Punkte..." können wir über den schwachen Außenwinkelsatz ausschließen, da es keine Dreiecke gibt, bei dem zwei Innenwinkel kongruent zu den Außenwinkel sind. Denn mit drei (verschiedenen) Punkten <math>\ Q, Q' und Q'' \in g</math> und den kongruenten Strecken <math>\overline {PQ}, \overline {PQ'} und \overline {PQ} </math> würden (o.B.d.A) zwei (gleichschenklige) Dreiecke <math>\overline {PQQ'} und \overline {PQ'Q''}</math> entstehen, deren Basis auf der selben Geraden <math>\ QQ''</math> liegt und bei denen der Außenwinkel des einen Innenwinkels <math>\ \alpha</math> von <math>\overline {PQQ'}</math>gleichzeitig der "andere" Innenwinkel <math>\ \beta'</math> von <math>\overline {PQ'Q''}</math> ist. Diese Winkel sind supplementäre Nebenwinkel und wären somit rechte Winkel. Nach der Dreieckskongruenz müsste nun auch der zweite Innenwinkel von <math>\overline {PQQ'}</math> (<math>\ \beta</math>) ein rechter Winkel sein. Dies ist nicht möglich! (siehe [[Lösung_von_Aufgabe_12.2| Aufgabe 12.2]]) | + | <br />Den Fall "Es existieren mehr als zwei Punkte..." können wir über den schwachen Außenwinkelsatz ausschließen, da es keine Dreiecke gibt, bei dem zwei Innenwinkel kongruent zu den Außenwinkel sind. Denn mit drei (verschiedenen) Punkten <math>\ Q, Q' und Q'' \in g</math> und den kongruenten Strecken <math>\overline {PQ}, \overline {PQ'} </math> und <math>\overline {PQ''} </math> würden (o.B.d.A) zwei (gleichschenklige) Dreiecke <math>\overline {PQQ'} und \overline {PQ'Q''}</math> entstehen, deren Basis auf der selben Geraden <math>\ QQ''</math> liegt und bei denen der Außenwinkel des einen Innenwinkels <math>\ \alpha</math> von <math>\overline {PQQ'}</math>gleichzeitig der "andere" Innenwinkel <math>\ \beta'</math> von <math>\overline {PQ'Q''}</math> ist. Diese Winkel sind supplementäre Nebenwinkel und wären somit rechte Winkel. Nach der Dreieckskongruenz müsste nun auch der zweite Innenwinkel von <math>\overline {PQQ'}</math> (<math>\ \beta</math>) ein rechter Winkel sein. Dies ist nicht möglich! (siehe [[Lösung_von_Aufgabe_12.2| Aufgabe 12.2]]) |
<br />Es bleiben Fall 1 und 2! | <br />Es bleiben Fall 1 und 2! | ||
|- | |- | ||
| Zeile 71: | Zeile 74: | ||
|- | |- | ||
! style="background: #FFDDDD;"|(V) | ! style="background: #FFDDDD;"|(V) | ||
| − | | In allen möglichen Fällen lassen sich zwei | + | | In allen möglichen Fällen lassen sich zwei Punkte <math>\ A \in g</math> und <math>\ B \in g</math> konstruieren, die zu <math>\ P \notin g</math> den selben Abstand haben! |
| (I) - (IV) | | (I) - (IV) | ||
|- | |- | ||
Version vom 15. Juli 2010, 02:32 Uhr
Beweisen Sie die Existenz und die Eindeutigkeit des Lotes von einem Punkt  auf eine Gerade
auf eine Gerade  .
.
Existenz
Voraussetzung: Gerade  , Punkt
, Punkt 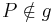
Behauptung: Es existiert ein Lot 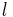 von
von  auf
auf  mit Lotfußpunkt
mit Lotfußpunkt 
Analoge Behauptung (Definition von Lot) Es existiert eine Senkrechte auf  , die durch
, die durch  geht.
geht.
Hilfskonstruktion: Es existieren zwei VERSCHIEDENE Punkte 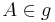 und
und 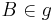 mit dem selben Abstand zu
mit dem selben Abstand zu 
Kommentar --*m.g.* 10:18, 13. Jul. 2010 (UTC): Begründen müssten Sie die Korrektheit der Hilfskonstruktion schon. Woher wissen Sie, dass die beiden Punkte  und
und  existieren?
existieren?
Re --Heinzvaneugen 00:32, 15. Jul. 2010 (UTC): Beweis wurde nun weiter unten aufgeführt. Funktioniert das so?
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 
|
Hilfskonstruktion, Axiom vom Lineal |
| (II) | Es existiert ein Mittelpunkt  der Strecke der Strecke 
|
Eindeutigkeit des Mittelpunktes |
| (III) | 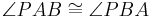
|
Gleichschenkliges Dreieck, Basiswinkelsatz |
| (IV) | 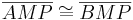
|
SWS - (I), (II), (III)
|
| (V) | 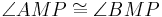
|
(IV), Dreieckskongruenz |
| (VI) | 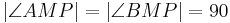
|
(V), Definition rechte Winkel: kongruente Nebenwinkel |
Es existiert ein Strahl 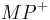 , der mit
, der mit 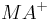 oder
oder 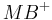 einen rechten Winkel bildet, anders ausgedrückt: Es existiert eine Senkrechte auf
einen rechten Winkel bildet, anders ausgedrückt: Es existiert eine Senkrechte auf  (da
(da 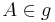 und
und 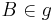 und
und 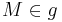 ), die durch
), die durch  geht.
geht.
zu Schritt (I): Im weiteren Beweis wird klar, was man schon länger vermutete: dass ein Punkt  zu entweder keinem, zu einem oder zu zwei Punkten einer Gerade
zu entweder keinem, zu einem oder zu zwei Punkten einer Gerade  einen bestimmten Abstand hat. Der Fall, dass wir eine Strecke von
einen bestimmten Abstand hat. Der Fall, dass wir eine Strecke von  auf dem Strahl
auf dem Strahl  antragen und keinen Schnittpunkt mit
antragen und keinen Schnittpunkt mit  erhalten, kann man schnell ad acta legen, macht keinen Sinn! Wenn es nur einen Punkt gibt, dann sind wir fertig, das ist das Lot (das kann später bewiesen werden).
erhalten, kann man schnell ad acta legen, macht keinen Sinn! Wenn es nur einen Punkt gibt, dann sind wir fertig, das ist das Lot (das kann später bewiesen werden).
Genau genommen ist der Schritt (1) also: Wir wählen einen beliebigen Punkt 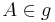 und tragen (nach Axiom vom Lineal) die Strecke
und tragen (nach Axiom vom Lineal) die Strecke 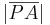 auf einem zweiten Strahl von
auf einem zweiten Strahl von  aus an und finden so den Punkt
aus an und finden so den Punkt 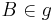 .
.
Falls es keinen zweiten Punkt gibt, wählen wir von diesem Punkt 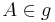 eine beliebige Strecke, die wir "auf der Geraden
eine beliebige Strecke, die wir "auf der Geraden  " abtragen und nun einen Punkt
" abtragen und nun einen Punkt 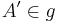 bekommen und in der anderen Halbebene bzgl.
bekommen und in der anderen Halbebene bzgl. 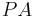 einen weiteren Punkt mit dem selben Abstand.
einen weiteren Punkt mit dem selben Abstand.
--Heinzvaneugen 00:27, 13. Jul. 2010 (UTC)
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | Es existiert eine Gerade  zwischen einem beliebigen Punkt zwischen einem beliebigen Punkt 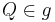 und dem Punkt und dem Punkt 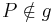
|
AXIOM I/1(Axiom von der Geraden) |
| (II) | Der Abstand 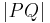 ist eindeutig (aber nicht eineindeutig) und meßbar ist eindeutig (aber nicht eineindeutig) und meßbar
|
Axiom III.1: (Axiom vom Lineal) |
| (III) | Fallunterscheidung:
|
Den Fall: "Es existiert kein Punkt..." haben wir in (I) und (II) ausgeschlossen.
|
| (IV) | weiter mit: Fall 1: Wenn es NUR EINEN Punkt 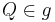 gibt, der den Abstand gibt, der den Abstand 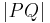 zu zu  hat, dann existieren die Punkte hat, dann existieren die Punkte 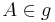 und und 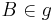 , die bezüglich der Geraden , die bezüglich der Geraden 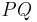 in unterschiedlichen Halbebenen liegen. Es gilt in unterschiedlichen Halbebenen liegen. Es gilt  . .
|
Existenz und Eindeutigkeit des Mittelpunktes, Axiom vom Lineal (Streckenantragen) |
| (V) | In allen möglichen Fällen lassen sich zwei Punkte 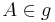 und und 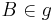 konstruieren, die zu konstruieren, die zu 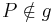 den selben Abstand haben! den selben Abstand haben!
|
(I) - (IV) |
Eindeutigkeit
Voraussetzung: Gerade  , Punkt
, Punkt 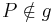 , Lot
, Lot 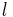 von
von  auf
auf  mit Lotfußpunkt
mit Lotfußpunkt 
Behauptung: Es existiert genau ein Lot von  auf
auf  .
.
Indirekter Beweis - Annahme: Es existieren zwei "Lote" von  auf
auf  .
.
Annahme: Es existiert ein zweiter Lotfußpunkt 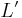
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | Es existiert ein Dreieck 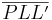
|
VSS, Punkte 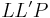 sind nicht kollinear, da sind nicht kollinear, da 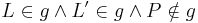 laut Definition Lot und Lotfußpunkt. laut Definition Lot und Lotfußpunkt.
|
| (II) | 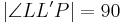
|
Annahme, 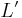 ist Lotfußpunkt ist Lotfußpunkt
|
| (III) | 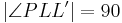
|
VSS,  ist Lotfußpunkt ist Lotfußpunkt
|
| (IV) | Außenwinkel von 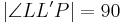
|
Supplementaxiom |
| (V) | 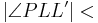 Außenwinkel von Außenwinkel von 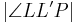
|
Schwacher Außenwinkelsatz |
| (VI) | Annahme muss verworfen werden | Widerspruch zwischen (V) und (III) !!! |
--Heinzvaneugen 00:27, 13. Jul. 2010 (UTC)
 (Definition Mittelpunkt) --> S
(Definition Mittelpunkt) --> S
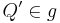 mit dem Abstand
mit dem Abstand 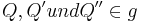 und den kongruenten Strecken
und den kongruenten Strecken 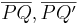 und
und 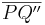 würden (o.B.d.A) zwei (gleichschenklige) Dreiecke
würden (o.B.d.A) zwei (gleichschenklige) Dreiecke 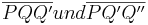 entstehen, deren Basis auf der selben Geraden
entstehen, deren Basis auf der selben Geraden 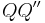 liegt und bei denen der Außenwinkel des einen Innenwinkels
liegt und bei denen der Außenwinkel des einen Innenwinkels  von
von 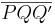 gleichzeitig der "andere" Innenwinkel
gleichzeitig der "andere" Innenwinkel 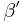 von
von 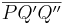 ist. Diese Winkel sind supplementäre Nebenwinkel und wären somit rechte Winkel. Nach der Dreieckskongruenz müsste nun auch der zweite Innenwinkel von
ist. Diese Winkel sind supplementäre Nebenwinkel und wären somit rechte Winkel. Nach der Dreieckskongruenz müsste nun auch der zweite Innenwinkel von  ) ein rechter Winkel sein. Dies ist nicht möglich! (siehe
) ein rechter Winkel sein. Dies ist nicht möglich! (siehe