Lösung von Aufgabe 12.4: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| Zeile 6: | Zeile 6: | ||
<br />Behauptung: Es existiert ein Lot <math>\ l</math>von <math>\ P</math> auf <math>\ g</math> mit Lotfußpunkt <math>\ L</math> | <br />Behauptung: Es existiert ein Lot <math>\ l</math>von <math>\ P</math> auf <math>\ g</math> mit Lotfußpunkt <math>\ L</math> | ||
<br />Analoge Behauptung (Definition von Lot) Es existiert eine Senkrechte auf <math>\ g</math>, die durch <math>\ P</math> geht. | <br />Analoge Behauptung (Definition von Lot) Es existiert eine Senkrechte auf <math>\ g</math>, die durch <math>\ P</math> geht. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | ! Nr. | ||
| + | ! Beweisschritt | ||
| + | ! Begründung | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(I) | ||
| + | | Es existiert ein Punkt <math>A \in g</math>, der Abstand zu P beträgt <math>|AP| \ </math> | ||
| + | | Axiom I/1 (Axiom von der Geraden), Axiom III.1 (Axiom vom Lineal) | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(II) | ||
| + | | tbc | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(III) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(IV) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(V) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(VI) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(VII) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(VIII) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(IX) | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(X) | ||
| + | | | ||
| + | | | ||
| + | |} | ||
<ggb_applet width="1116" height="616" version="3.2" ggbBase64="UEsDBBQACAAIAPhW9DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VvbjuO2Gb5unoLwRdAWa4+ok2VkZgN3UjQLOF0jk26B3AxoiZa5lilHombseZ4+QBb7Bu39PlN/HuSDLHt9mllvjAEkk79I/t/3n0h5rr+fTRL0QLOcpfymgVtWA1EephHj8U2jEMNm0Pj+9TfXMU1jOsgIGqbZhIibhtOyG7K9YK+/+dN1PkofEUmUyDtGH28aQ5LktIHyaUZJlI8oFWvtpJixhJFs/nbwnoYiX3boQd7waQGziKyAtnAS9Vhefr1SE04TJn5gDyyiGUrS8Kbhe7B0uHtHM8FCktw0XEu32DcNu9IJTY7sHaUZe0q5kOLLwYfQglDOniggYsu26yul6DUtwoRFjHCpjFoHCCH0yCIxAlnH92FMyuIRLNbHrh4uTNMsupvngk7Q7FeapbC0Dm7hwG4HnuVg+LPdBprrLscHEpx223Ux9vzA6XiAIiwZ1uLZLQ9bnmsHvm+3LUs+tLVLTU0f7qgQwGWOyIwuUY4zFpXoyvs3+d/SJFp0T1PGxS2ZiiJTduCYpjsxl5MBcJnUscvjhJo2G2ga0XA8SGd3GjhHD/3LfKoeUesZxLdpkmYok5SAYrG5DvRVyciFLqQsJWMpCTOGHHTRjzu2klDXgb4qqYRxvTSjOC6VxlY5DcuRbIDBpfkulE/IgII5NFDBmeiVX8BsxkZVrB/4ZzEZgN+sGs5iTHyuMa+vKiZ3PaYZp4m2Kw7UFmmRowdpwHoutZCIhmwCX3WHgYRIuv4FC9CtEY0zWi5ce50GTPVaq7Zbab6+Khch15DDWkMB4QP0EVIX6d0CPOum8SNl/OmBcFrElDdQRITsln6U0AkFJxPKOJRtLUDqNxYRJVXBoTRU07+EGyaPmJpZSr81wvE91t3wdK0dKYsjyXREoKVlFE3IHCLJqupqup/SaB0QwgFYPaegUzmApG5KaWSipzD2jqYwpPKeFV4UnDmayfgJInOIBPL6pJ9VItrRZFhR0zrGCjRgn4GueyJ0o/MB93Y4zKmQmjZxR2naxC+Bq2VwxefE9XYT13XHXgJ70UYXHAtOmE4mhEeIkwnM04PYqhBhMksjYknLQwRLoDQIhSg7Yj2UGWADZxmmFyjGjfXILUYQIDnNc5VexGoiecbwYB3P06YZBgbpZrAYax/16G9cy+Q6PbAJ1DshE7t5Ufm4QsytJkbyY8vYWuXn04fdBKmksQAXpOXzoHNRat6CIsbpBNh3nA4ULYFzKkFsGz3Y2iQI7xuEbE8HIcepJRAfQA7JwhVXKRuTJH38mQ4TOlM06N6VNL6Fszsay/YKa/2StSpdg91s5Wa0EuvBOTxqLZQckTbO4lBlvmw6xqOcszmUAjiRYfMNF1B9UVXNbBZVY0qnspp9y3/JCM/lTmhfln9OBdQ+9a7pYK9l/fW/v2sP3aT89lsyTfPvdhNfyVfmkb2z1t6e6LuKWHkZ6Mvp1HotHzY6sHdxO27HdtqmXHDXmwPsnZKzamOjgWk1Qm5msE8f9iGgGidXGNgVLb2LjpZOPYNfLFjesizcYNGUHpupje5mDPBk4QJnukektE8Ple+fLVTut3TKYCf2AEtJsxyhmWVqwbllSpansmUGkDZ1FYPLghGveB/UoxmboW4p3y2lurYs9dsta+0DgaLrmDm6bjl015OyrS0xGgrckA2Bo2OL0aXfrtlFeEBJGp7FLI524jMmUK8mnM5rg68sVzebDzGyo6rXRfKtsEk1m6GOz3aJwAqh/cMzZH9bhjyItxpvPjpBrkRfVwffnfvlJbF2q7P+8XX+tCsuiE9Jn/Vlahl6tzhadFixGr1Isfp8EXitWK1CP68n6kkRtdH+1RS2O7cv2+xieJhdDF/ELsYvYBd+rV1Apeu6VtCxrU7gWZZv+39vYmMb+HznBi9gDdtCeKztYbhhCb1DYnbvxGhdw/AZonVb+7a/nwVg1y0PfoNW1Rae6lrPtNcxLtnbtsv89PGg/c3H6s4Gt7y21e74ju23O27Q8YNTiyL+HDsbOzBn0fV8veDOZh3eQZomlPDlUeg9riK84qL7gHp6IFui5puawt1dkpCpIlG19Qs+Fqj/Cv2DZgQE48P0H12g9m37QO27iBRDFL9CdyKj4Ziibv8wFNhFoaAjHbbqT1DrYPg342OaoE8fEJmgu3BEmaDJ1GDDOPqRJAM6oBzM41W/ichAZES+KTwIpPcXBZI2Fezsbyvv4EZaSv5KmYv8QcO3vxWp+I7TgnJ9a7yo/BYxinr/+w+PqRJfmteREI4vCkJjZ2UG2cfdTKWJ8nDEKYtgpFjaV293nuynyTxO+bbzJJUpexuZ8h2D8cIx1mKJFiP38rsDJcvnKho9ZYnhYrCXKHEnm2xhz1F8efjAlFohZLutVav55EhV14+uV3TdU52ji/Zm+eqhfPPQvPBXD7vxJ/fHGtsXY2Dx7mfHRimobKKDr5eh6dfGT/myu+4kQ5LzNR9w1OeI/uqbo617KhPcbS1G7m0tOF08DPki0T9HODhj2F8qY+j8blt6y6yuz50yJHLP6BK7NDopa9Sc9Vgmh3QqvRu/Wrwkj/hMuFo5Sv+aGPpjRa3PFF3Pm/SfhZ8/8iH67u3Y5BK3Y539t2O/PlKGximPYUWAGfoho0xtUPu9LiogtZr02esehgu/KFz0Tt/e8oOyXcchH9GfzW231/8LYrlAFHarsIkfgYUh3VeF5mr1p9bqPxLMv2S8/j9QSwcI9WXe0vQHAADEMQAAUEsBAhQAFAAIAAgA+Fb0PPVl3tL0BwAAxDEAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAAuCAAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | <ggb_applet width="1116" height="616" version="3.2" ggbBase64="UEsDBBQACAAIAPhW9DwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VvbjuO2Gb5unoLwRdAWa4+ok2VkZgN3UjQLOF0jk26B3AxoiZa5lilHombseZ4+QBb7Bu39PlN/HuSDLHt9mllvjAEkk79I/t/3n0h5rr+fTRL0QLOcpfymgVtWA1EephHj8U2jEMNm0Pj+9TfXMU1jOsgIGqbZhIibhtOyG7K9YK+/+dN1PkofEUmUyDtGH28aQ5LktIHyaUZJlI8oFWvtpJixhJFs/nbwnoYiX3boQd7waQGziKyAtnAS9Vhefr1SE04TJn5gDyyiGUrS8Kbhe7B0uHtHM8FCktw0XEu32DcNu9IJTY7sHaUZe0q5kOLLwYfQglDOniggYsu26yul6DUtwoRFjHCpjFoHCCH0yCIxAlnH92FMyuIRLNbHrh4uTNMsupvngk7Q7FeapbC0Dm7hwG4HnuVg+LPdBprrLscHEpx223Ux9vzA6XiAIiwZ1uLZLQ9bnmsHvm+3LUs+tLVLTU0f7qgQwGWOyIwuUY4zFpXoyvs3+d/SJFp0T1PGxS2ZiiJTduCYpjsxl5MBcJnUscvjhJo2G2ga0XA8SGd3GjhHD/3LfKoeUesZxLdpkmYok5SAYrG5DvRVyciFLqQsJWMpCTOGHHTRjzu2klDXgb4qqYRxvTSjOC6VxlY5DcuRbIDBpfkulE/IgII5NFDBmeiVX8BsxkZVrB/4ZzEZgN+sGs5iTHyuMa+vKiZ3PaYZp4m2Kw7UFmmRowdpwHoutZCIhmwCX3WHgYRIuv4FC9CtEY0zWi5ce50GTPVaq7Zbab6+Khch15DDWkMB4QP0EVIX6d0CPOum8SNl/OmBcFrElDdQRITsln6U0AkFJxPKOJRtLUDqNxYRJVXBoTRU07+EGyaPmJpZSr81wvE91t3wdK0dKYsjyXREoKVlFE3IHCLJqupqup/SaB0QwgFYPaegUzmApG5KaWSipzD2jqYwpPKeFV4UnDmayfgJInOIBPL6pJ9VItrRZFhR0zrGCjRgn4GueyJ0o/MB93Y4zKmQmjZxR2naxC+Bq2VwxefE9XYT13XHXgJ70UYXHAtOmE4mhEeIkwnM04PYqhBhMksjYknLQwRLoDQIhSg7Yj2UGWADZxmmFyjGjfXILUYQIDnNc5VexGoiecbwYB3P06YZBgbpZrAYax/16G9cy+Q6PbAJ1DshE7t5Ufm4QsytJkbyY8vYWuXn04fdBKmksQAXpOXzoHNRat6CIsbpBNh3nA4ULYFzKkFsGz3Y2iQI7xuEbE8HIcepJRAfQA7JwhVXKRuTJH38mQ4TOlM06N6VNL6Fszsay/YKa/2StSpdg91s5Wa0EuvBOTxqLZQckTbO4lBlvmw6xqOcszmUAjiRYfMNF1B9UVXNbBZVY0qnspp9y3/JCM/lTmhfln9OBdQ+9a7pYK9l/fW/v2sP3aT89lsyTfPvdhNfyVfmkb2z1t6e6LuKWHkZ6Mvp1HotHzY6sHdxO27HdtqmXHDXmwPsnZKzamOjgWk1Qm5msE8f9iGgGidXGNgVLb2LjpZOPYNfLFjesizcYNGUHpupje5mDPBk4QJnukektE8Ple+fLVTut3TKYCf2AEtJsxyhmWVqwbllSpansmUGkDZ1FYPLghGveB/UoxmboW4p3y2lurYs9dsta+0DgaLrmDm6bjl015OyrS0xGgrckA2Bo2OL0aXfrtlFeEBJGp7FLI524jMmUK8mnM5rg68sVzebDzGyo6rXRfKtsEk1m6GOz3aJwAqh/cMzZH9bhjyItxpvPjpBrkRfVwffnfvlJbF2q7P+8XX+tCsuiE9Jn/Vlahl6tzhadFixGr1Isfp8EXitWK1CP68n6kkRtdH+1RS2O7cv2+xieJhdDF/ELsYvYBd+rV1Apeu6VtCxrU7gWZZv+39vYmMb+HznBi9gDdtCeKztYbhhCb1DYnbvxGhdw/AZonVb+7a/nwVg1y0PfoNW1Rae6lrPtNcxLtnbtsv89PGg/c3H6s4Gt7y21e74ju23O27Q8YNTiyL+HDsbOzBn0fV8veDOZh3eQZomlPDlUeg9riK84qL7gHp6IFui5puawt1dkpCpIlG19Qs+Fqj/Cv2DZgQE48P0H12g9m37QO27iBRDFL9CdyKj4Ziibv8wFNhFoaAjHbbqT1DrYPg342OaoE8fEJmgu3BEmaDJ1GDDOPqRJAM6oBzM41W/ichAZES+KTwIpPcXBZI2Fezsbyvv4EZaSv5KmYv8QcO3vxWp+I7TgnJ9a7yo/BYxinr/+w+PqRJfmteREI4vCkJjZ2UG2cfdTKWJ8nDEKYtgpFjaV293nuynyTxO+bbzJJUpexuZ8h2D8cIx1mKJFiP38rsDJcvnKho9ZYnhYrCXKHEnm2xhz1F8efjAlFohZLutVav55EhV14+uV3TdU52ji/Zm+eqhfPPQvPBXD7vxJ/fHGtsXY2Dx7mfHRimobKKDr5eh6dfGT/myu+4kQ5LzNR9w1OeI/uqbo617KhPcbS1G7m0tOF08DPki0T9HODhj2F8qY+j8blt6y6yuz50yJHLP6BK7NDopa9Sc9Vgmh3QqvRu/Wrwkj/hMuFo5Sv+aGPpjRa3PFF3Pm/SfhZ8/8iH67u3Y5BK3Y539t2O/PlKGximPYUWAGfoho0xtUPu9LiogtZr02esehgu/KFz0Tt/e8oOyXcchH9GfzW231/8LYrlAFHarsIkfgYUh3VeF5mr1p9bqPxLMv2S8/j9QSwcI9WXe0vQHAADEMQAAUEsBAhQAFAAIAAgA+Fb0PPVl3tL0BwAAxDEAAAwAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAQABADoAAAAuCAAAAAA=" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /> | ||
Version vom 20. Juli 2010, 11:55 Uhr
Beweisen Sie die Existenz und die Eindeutigkeit des Lotes von einem Punkt  auf eine Gerade
auf eine Gerade  .
.
Existenz
Voraussetzung: Gerade  , Punkt
, Punkt 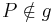
Behauptung: Es existiert ein Lot 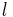 von
von  auf
auf  mit Lotfußpunkt
mit Lotfußpunkt 
Analoge Behauptung (Definition von Lot) Es existiert eine Senkrechte auf  , die durch
, die durch  geht.
geht.
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | Es existiert ein Punkt 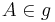 , der Abstand zu P beträgt , der Abstand zu P beträgt 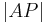
|
Axiom I/1 (Axiom von der Geraden), Axiom III.1 (Axiom vom Lineal) |
| (II) | tbc | |
| (III) | ||
| (IV) | ||
| (V) | ||
| (VI) | ||
| (VII) | ||
| (VIII) | ||
| (IX) | ||
| (X) |
Eindeutigkeit
Voraussetzung: Gerade  , Punkt
, Punkt 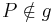 , Lot
, Lot 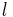 von
von  auf
auf  mit Lotfußpunkt
mit Lotfußpunkt 
Behauptung: Es existiert genau ein Lot von  auf
auf  .
.
Indirekter Beweis - Annahme: Es existieren zwei "Lote" von  auf
auf  .
.
Annahme: Es existiert ein zweiter Lotfußpunkt 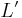
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | Es existiert ein Dreieck 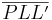
|
VSS, Punkte 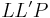 sind nicht kollinear, da sind nicht kollinear, da 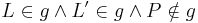 laut Definition Lot und Lotfußpunkt. laut Definition Lot und Lotfußpunkt.
|
| (II) | 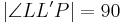
|
Annahme, 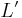 ist Lotfußpunkt ist Lotfußpunkt
|
| (III) | 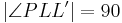
|
VSS,  ist Lotfußpunkt ist Lotfußpunkt
|
| (IV) | Außenwinkel von 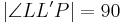
|
Supplementaxiom |
| (V) | 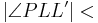 Außenwinkel von Außenwinkel von 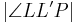
|
Schwacher Außenwinkelsatz |
| (VI) | Annahme muss verworfen werden | Widerspruch zwischen (V) und (III) !!! |
--Heinzvaneugen 00:27, 13. Jul. 2010 (UTC)