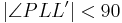Lösung von Aufgabe 12.4
Beweisen Sie die Existenz und die Eindeutigkeit des Lotes von einem Punkt  auf eine Gerade
auf eine Gerade  .
.
Existenz
Voraussetzung: Gerade  , Punkt
, Punkt 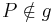
Behauptung: Es existiert ein Lot 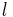 von
von  auf
auf  mit Lotfußpunkt
mit Lotfußpunkt 
Analoge Behauptung (Definition von Lot) Es existiert eine Senkrechte auf  , die durch
, die durch  geht.
geht.
Hilfskonstruktion: Es existieren zwei VERSCHIEDENE Punkte 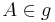 und
und 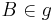 mit dem selben Abstand zu
mit dem selben Abstand zu 
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 
|
Hilfskonstruktion, Axiom vom Lineal |
| (II) | Es existiert ein Mittelpunkt  der Strecke der Strecke 
|
Eindeutigkeit des Mittelpunktes |
| (III) | 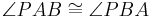
|
Gleichschenkliges Dreieck |
| (IV) | 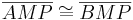
|
SWS - (I), (II), (III)
|
| (V) | 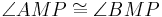
|
(IV), Dreieckskongruenz |
| (VI) | 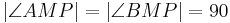
|
(V), Definition rechte Winkel: kongruente Nebenwinkel |
Es existiert ein Strahl 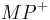 , der mit
, der mit 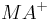 oder
oder 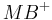 einen rechten Winkel bildet, anders ausgedrückt: Es existiert eine Senkrechte auf
einen rechten Winkel bildet, anders ausgedrückt: Es existiert eine Senkrechte auf  (da
(da 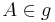 und
und 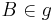 ), die durch
), die durch  geht.
geht.
zu Schritt (I): Es ist ein leichtes (sag ich mal so), zu beweisen, dass ein Punkt  zu entweder keinem, zu einem oder zu zwei Punkten einer Gerade
zu entweder keinem, zu einem oder zu zwei Punkten einer Gerade  einen bestimmten Abstand hat. Der Fall, dass wir eine Strecke von
einen bestimmten Abstand hat. Der Fall, dass wir eine Strecke von  auf dem Strahl
auf dem Strahl  antragen und keinen Schnittpunkt mit
antragen und keinen Schnittpunkt mit  erhalten, kann man schnell ad acta legen, macht keinen Sinn! Wenn es nur einen Punkt gibt, dann sind wir fertig, das ist das Lot (das kann später bewiesen werden). Genau genommen ist der Schritt (1) also: Wir wählen einen beliebigen Punkt
erhalten, kann man schnell ad acta legen, macht keinen Sinn! Wenn es nur einen Punkt gibt, dann sind wir fertig, das ist das Lot (das kann später bewiesen werden). Genau genommen ist der Schritt (1) also: Wir wählen einen beliebigen Punkt 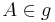 und tragen (nach Axiom vom Lineal) die Strecke
und tragen (nach Axiom vom Lineal) die Strecke 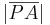 auf einem beliebigen zweiten Strahl
auf einem beliebigen zweiten Strahl 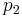 von
von  aus an und finden so den Punkt
aus an und finden so den Punkt 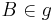
--Heinzvaneugen 00:27, 13. Jul. 2010 (UTC)
Eindeutigkeit
Voraussetzung: Gerade  , Punkt
, Punkt 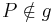 , Lot
, Lot 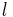 von
von  auf
auf  mit Lotfußpunkt
mit Lotfußpunkt 
Behauptung: Es existiert genau ein Lot von  auf
auf  .
.
Indirekter Beweis - Annahme: Es existieren zwei "Lote" von  auf
auf  .
.
Annahme: Es existiert ein zweiter Lotfußpunkt 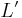
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | Es existiert ein Dreieck 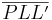
|
VSS, Punkte 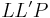 sind nicht kollinear, da sind nicht kollinear, da 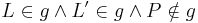 laut Definition Lot und Lotfußpunkt. laut Definition Lot und Lotfußpunkt.
|
| (II) | 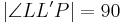
|
Annahme, 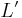 ist Lotfußpunkt ist Lotfußpunkt
|
| (III) | 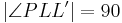
|
VSS,  ist Lotfußpunkt ist Lotfußpunkt
|
| (IV) | Außenwinkel von 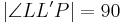
|
Supplementaxiom |
| (V) | 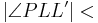 Außenwinkel von Außenwinkel von 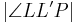
|
Schwacher Außenwinkelsatz |
| (VI) | Annahme muss verworfen werden | Widerspruch zwischen (V) und (III) !!! |
--Heinzvaneugen 00:27, 13. Jul. 2010 (UTC)
 (Definition Mittelpunkt) --> S
(Definition Mittelpunkt) --> S