Lösung von Aufgabe 12.4
Beweisen Sie die Existenz und die Eindeutigkeit des Lotes von einem Punkt  auf eine Gerade
auf eine Gerade  .
.
Existenz
Voraussetzung: Gerade  , Punkt
, Punkt 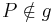
Behauptung: Es existiert ein Lot 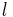 von
von  auf
auf  mit Lotfußpunkt
mit Lotfußpunkt 
Analoge Behauptung (Definition von Lot) Es existiert eine Senkrechte auf  , die durch
, die durch  geht.
geht.
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | Es existiert ein Punkt 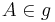 , der Abstand zu P beträgt , der Abstand zu P beträgt 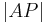
|
Axiom I/1 (Axiom von der Geraden), Axiom III.1 (Axiom vom Lineal) |
| (II) | Am Scheitelpunkt 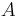 wird an der Gerade wird an der Gerade 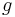 der Winkel der Winkel 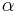 in die Halbebene in die Halbebene 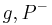 abgetragen. abgetragen.
|
Winkelkonstruktionsaxiom |
| (III) | Auf dem entstanden Strahl trägt man die Länge von 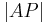 ab. Es entsteht der Punkt ab. Es entsteht der Punkt  . .
|
Axiom III.1 (Axiom vom Lineal) |
| (IV) | 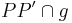 . Der Schnittpunkt sei . Der Schnittpunkt sei  . .
|
 und und  liegen in unterschiedlichen Halbebenen bezogen auf liegen in unterschiedlichen Halbebenen bezogen auf  . .
|
| (V) | Es entstehen zwei kongruente Dreiecke 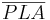 und und 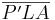
|
SWS
S - |
| (VI) | Die Winkel an  sind rechte Winkel sind rechte Winkel
|
(IV), (V), kongruente Nebenwinkel sind rechte Winkel (Definition V.6 : Rechter Winkel) |
| (VII) | 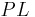 steht senkrecht auf steht senkrecht auf 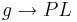 ist Lotgerade, ist Lotgerade, 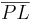 ist Lot(strecke) ist Lot(strecke)
|
(VI), Definition Lot |
Kleine Anmerkung: Bei Schritt (II) muss man an sich auch definieren, dass der Winkel 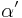 bezüglich
bezüglich 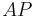 in der selben Halbebene liegt wie
in der selben Halbebene liegt wie 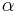 . An dieser Stelle wurde es wg. besserer Übersicht weggelassen.
. An dieser Stelle wurde es wg. besserer Übersicht weggelassen.
Eindeutigkeit
Voraussetzung: Gerade  , Punkt
, Punkt 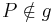 , Lot
, Lot 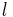 von
von  auf
auf  mit Lotfußpunkt
mit Lotfußpunkt 
Behauptung: Es existiert genau ein Lot von  auf
auf  .
.
Indirekter Beweis - Annahme: Es existieren zwei "Lote" von  auf
auf  .
.
Annahme: Es existiert ein zweiter Lotfußpunkt 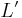
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | Es existiert ein Dreieck 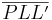
|
VSS, Punkte 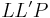 sind nicht kollinear, da sind nicht kollinear, da 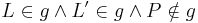 laut Definition Lot und Lotfußpunkt. laut Definition Lot und Lotfußpunkt.
|
| (II) | 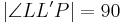
|
Annahme, 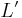 ist Lotfußpunkt ist Lotfußpunkt
|
| (III) | 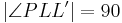
|
VSS,  ist Lotfußpunkt ist Lotfußpunkt
|
| (IV) | Außenwinkel von 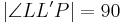
|
Supplementaxiom |
| (V) | 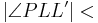 Außenwinkel von Außenwinkel von 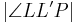
|
Schwacher Außenwinkelsatz |
| (VI) | Annahme muss verworfen werden | Widerspruch zwischen (V) und (III) !!! |
--Heinzvaneugen 00:27, 13. Jul. 2010 (UTC)
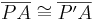 (III)
(III)
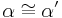 (II)
(II)
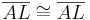 trivial
trivial