Lösung von Aufgabe 13.3P (WS 18/19): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
CIG UA (Diskussion | Beiträge) |
CIG UA (Diskussion | Beiträge) |
||
| Zeile 6: | Zeile 6: | ||
1.) <math>\overline{ABC}</math> mit {A} = g geschnitten h und B ε g und C ε h<br /> | 1.) <math>\overline{ABC}</math> mit {A} = g geschnitten h und B ε g und C ε h<br /> | ||
2.) D<sub>H,180</sub> (<math>\overline{ABC}</math>) = <math>\overline{A'B'C'}</math> mit H ε h und A' ε h '''- Def. Punktspiegelung'''<br /> | 2.) D<sub>H,180</sub> (<math>\overline{ABC}</math>) = <math>\overline{A'B'C'}</math> mit H ε h und A' ε h '''- Def. Punktspiegelung'''<br /> | ||
| − | 3.) |α| = |α'| mit|α|= |<(BAC)| und |α'|= |<(B'A'C')| '''- Winkelmaßerhaltung, Vor: | + | 3.) |α| = |α'| mit|α|= |<(BAC)| und |α'|= |<(B'A'C')| '''- Winkelmaßerhaltung, Vor: α und α' sind Wechselwinkel'''<br /> |
4.) A = g geschnitten h => A' = g' geschnitten h' '''- Eigenschaft Spiegelung'''<br /> | 4.) A = g geschnitten h => A' = g' geschnitten h' '''- Eigenschaft Spiegelung'''<br /> | ||
5.) H ε h => h = h' und g' = D<sub>H,180</sub>(g) => g || g' '''- Eigenschaft Punktspiegelung (Parallelenerzeugung)'''<br /> | 5.) H ε h => h = h' und g' = D<sub>H,180</sub>(g) => g || g' '''- Eigenschaft Punktspiegelung (Parallelenerzeugung)'''<br /> | ||
Aktuelle Version vom 30. Januar 2019, 00:36 Uhr
Beweisen Sie die Umkehrung des Wechselwinkelsatzes mit abbildungsgeometrischen Methoden. Hinweis: Der Wechselwinkelsatz ist bereits bewiesen.
Vor: Wechselwinkel sind gleich groß; Beh: => Geschnittene Seiten sind parallel
1.) 
mit {A} = g geschnitten h und B ε g und C ε h
2.) DH,180 () = 
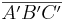mit H ε h und A' ε h - Def. Punktspiegelung
3.) |α| = |α'| mit|α|= |<(BAC)| und |α'|= |<(B'A'C')| - Winkelmaßerhaltung, Vor: α und α' sind Wechselwinkel
4.) A = g geschnitten h => A' = g' geschnitten h' - Eigenschaft Spiegelung
5.) H ε h => h = h' und g' = DH,180(g) => g || g' - Eigenschaft Punktspiegelung (Parallelenerzeugung)
Die Behauptung gilt.--CIG UA (Diskussion) 13:47, 25. Jan. 2019 (CET)
