Lösung von Aufgabe 2.6 S (SoSe 12)
Aufgabe 2.6
Bringen Sie die folgenden Implikationen in die Form Wenn-Dann:
- Jedes Quadrat hat vier rechte Innenwinkel.
- Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt auf der Hypotenuse dieses Dreiecks.
- In einem konvexen Viereck schneiden sich die Diagonalen des Vierecks.
- Die Geraden, die durch die Diagonalen einer Raute
 eindeutig bestimmt sind, sind Symmetrieachsen von
eindeutig bestimmt sind, sind Symmetrieachsen von  .
.
- Es sei
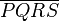 ein Paralellogramm. Es gilt:
ein Paralellogramm. Es gilt: 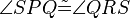 .
.
- Die Innenwinkelsumme im Dreieck beträgt 180°.
1. Wenn  ein Quadrat ist, dann hat es vier rechte Innenwinkel.
ein Quadrat ist, dann hat es vier rechte Innenwinkel.
2. Wenn der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks bestimmt wird, dann liegt dieser auf der Hypothenuse dieses Dreiecks.
3. Wenn ein Viereck konvex ist, dann schneiden sich seine Diagonalen.
4. Wenn die Diagonalen einer Raute  durch Geraden eindeutig bestimmt sind, dann sind dies Symmetrieachsen von
durch Geraden eindeutig bestimmt sind, dann sind dies Symmetrieachsen von  .
.
5. Wenn 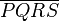 ein Paralellogramm ist, dann sind seine Winkel
ein Paralellogramm ist, dann sind seine Winkel 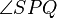 und
und 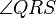 konkruent zueinander.
konkruent zueinander.
6. Wenn  ein Dreieck ist, dann beträgt seine Innenwinkelsumme 180°.
ein Dreieck ist, dann beträgt seine Innenwinkelsumme 180°.
von Wehnerj
Wehnerj - bitte immer dein Kürzel hinter deine Beiträge schreiben, damit man sich darauf beziehen kann.
Das sind gut und weniger gute Formulierungen dabei, was meinen die anderen?--Tutorin Anne 10:44, 28. Apr. 2012 (CEST)
- Ich habe mal ein paar mathematische Schreibweisen eingefügt, damit ihr sehen könnt, wie diese in LaTex geschrieben werden.--Tutor Andreas 16:05, 29. Apr. 2012 (CEST)
3. Wenn ein Dreieck rechtwinklig ist, dann liegt der Mittelpunkt seines Umkreises auf der Hypothenuse dieses Dreiecks.--Oz44oz 20:09, 28. Apr. 2012 (CEST)
4. Wenn die Diagonalen einer Raute  die Geraden eindeutig bestimmen, dann sind die Geraden Symmetrieachsen von
die Geraden eindeutig bestimmen, dann sind die Geraden Symmetrieachsen von  .--Goliath 13:38, 29. Apr. 2012 (CEST)
.--Goliath 13:38, 29. Apr. 2012 (CEST)

