Lösung von Aufgabe 2.9 SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="backgro…“) |
*m.g.* (Diskussion | Beiträge) (→Beweis) |
||
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
<!--- Was hier drüber steht muss stehen bleiben ---> | <!--- Was hier drüber steht muss stehen bleiben ---> | ||
| + | =Aufgabe 2.9 SoSe 2018= | ||
| + | Wir setzen ebene Geometrie voraus.<br /> | ||
| + | '''Satz: Tangentenkriterium'''<br /> | ||
| + | : Es seien <math>g</math> eine Gerade und <math>k</math> ein Kreis mit dem Mittelpunkt <math>M</math>. Ferner sei <math>B</math> ein Punkt, den die Gerade <math>g</math> mit dem Kreis <math>k</math> gemeinsam hat. <br /> | ||
| + | : (*) <math>k \cap g = \{B\} \Leftrightarrow g \perp \overline{MB} </math> | ||
| + | a) Aussage (*) beinhaltet zwei Aussagen <math>(\Rightarrow</math> und <math>\Leftarrow )</math>. Formulieren Sie beide Aussagen so, dass sie auch Schüler einer neunten Klasse Werkrealschule verstehen können.<br /> | ||
| + | b) Beweisen Sie die Aussage <math>\Leftarrow </math> mittels eines Widerspruchsbeweises.<br /> | ||
| + | =Lösung= | ||
| + | ==Teilaufgabe a)== | ||
| + | # Wenn eine Gerade Tangente <math>t</math> im Punkt <math>B</math> an den Kreis <math>k</math> mit dem Mittelpunkt <math>M</math> ist, dann steht <math>t</math> senkrecht auf dem Berührungsradius <math> ~\overline{MB}</math>. | ||
| + | # Wenn eine Gerade <math>t</math> den Kreis <math>k</math> mit dem Mittelpunkt <math>M</math> im Punkt <math>B</math> schneidet und senkrecht auf der Strecke <math> ~\overline{MB}</math> steht, dann ist die gerade <math>t</math> Tangente an den Kreis <math>k</math>. | ||
| + | ==Teilaufgabe b)== | ||
| + | ===Voraussetzung=== | ||
| + | <math> | ||
| + | \begin{matrix} | ||
| + | \text{I} & B \in t \land B \in k \\ | ||
| + | \text{II} & t \perp \overline{MB} \\ | ||
| + | \end{matrix} | ||
| + | </math> | ||
| + | ===Behauptung=== | ||
| + | <math>\neg \exist A \in k \cap t : A \not\equiv B</math> | ||
| + | ===Annahme=== | ||
| + | <math> \exist A \in k \cap t : A \not\equiv B</math> | ||
| + | ===Beweis=== | ||
| + | Das Dreieck <math>\overline{ABM}</math> ist gleichschenklig, weil <math>~\overline{MA}</math> und <math>~\overline{MB}</math> Radien von <math>k</math> sind. Die Winkel <math>\angle MBA</math> und <math>\angle MAB</math> sind die Basiwinkel dieses Dreiecks. Weil nach <math>\text{II}</math> der Winkel <math>\angle MBA</math> ein Rechter ist muss nach dem Basiswinkelsatz auch der Winkel <math>\angle MAB </math> ein Rechter sein. Das wäre jedoch ein Widerspruch zum Innenwinkelsatz für Dreiecke. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
Aktuelle Version vom 22. Mai 2018, 13:49 Uhr
Aufgabe 2.9 SoSe 2018Wir setzen ebene Geometrie voraus.
a) Aussage (*) beinhaltet zwei Aussagen LösungTeilaufgabe a)
Teilaufgabe b)Voraussetzung
Behauptung
Annahme
BeweisDas Dreieck |
 eine Gerade und
eine Gerade und  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  . Ferner sei
. Ferner sei  ein Punkt, den die Gerade
ein Punkt, den die Gerade 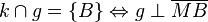
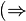 und
und 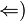 . Formulieren Sie beide Aussagen so, dass sie auch Schüler einer neunten Klasse Werkrealschule verstehen können.
. Formulieren Sie beide Aussagen so, dass sie auch Schüler einer neunten Klasse Werkrealschule verstehen können.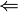 mittels eines Widerspruchsbeweises.
mittels eines Widerspruchsbeweises. im Punkt
im Punkt 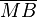 .
.
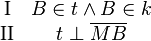
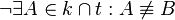
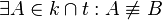
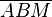 ist gleichschenklig, weil
ist gleichschenklig, weil 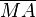 und
und 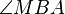 und
und 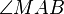 sind die Basiwinkel dieses Dreiecks. Weil nach
sind die Basiwinkel dieses Dreiecks. Weil nach 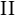 der Winkel
der Winkel 
