Aufgabe 2.9 SoSe 2018
Wir setzen ebene Geometrie voraus.
Satz: Tangentenkriterium
- Es seien
 eine Gerade und eine Gerade und  ein Kreis mit dem Mittelpunkt ein Kreis mit dem Mittelpunkt  . Ferner sei . Ferner sei  ein Punkt, den die Gerade ein Punkt, den die Gerade  mit dem Kreis mit dem Kreis  gemeinsam hat. gemeinsam hat.
- (*)
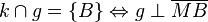
a) Aussage (*) beinhaltet zwei Aussagen 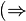 und und 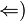 . Formulieren Sie beide Aussagen so, dass sie auch Schüler einer neunten Klasse Werkrealschule verstehen können. . Formulieren Sie beide Aussagen so, dass sie auch Schüler einer neunten Klasse Werkrealschule verstehen können.
b) Beweisen Sie die Aussage 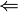 mittels eines Widerspruchsbeweises. mittels eines Widerspruchsbeweises.
Lösung
Teilaufgabe a)
- Wenn eine Gerade Tangente
 im Punkt im Punkt  an den Kreis an den Kreis  mit dem Mittelpunkt mit dem Mittelpunkt  ist, dann steht ist, dann steht  senkrecht auf dem Berührungsradius senkrecht auf dem Berührungsradius 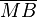 . .
- Wenn eine Gerade
 den Kreis den Kreis  mit dem Mittelpunkt mit dem Mittelpunkt  im Punkt im Punkt  schneidet und senkrecht auf der Strecke schneidet und senkrecht auf der Strecke 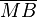 steht, dann ist die gerade steht, dann ist die gerade  Tangente an den Kreis Tangente an den Kreis  . .
Teilaufgabe b)
Voraussetzung
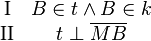
Behauptung
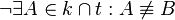
Annahme
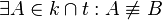
Beweis
Das Dreieck 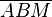 ist gleichschenklig, weil ist gleichschenklig, weil 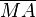 und und 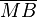 Radien von Radien von  sind. Die Winkel sind. Die Winkel 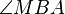 und und 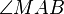 sind die Basiwinkel dieses Dreiecks. Weil nach sind die Basiwinkel dieses Dreiecks. Weil nach 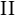 der Winkel der Winkel 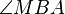 ein Rechter ist muss nach dem Basiswinkelsatz auch der Winkel ein Rechter ist muss nach dem Basiswinkelsatz auch der Winkel 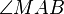 ein Rechter sein. Das wäre jedoch ein Widerspruch zum Innenwinkelsatz für Dreiecke. ein Rechter sein. Das wäre jedoch ein Widerspruch zum Innenwinkelsatz für Dreiecke.
|
 eine Gerade und
eine Gerade und  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  . Ferner sei
. Ferner sei  ein Punkt, den die Gerade
ein Punkt, den die Gerade 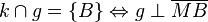
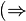 und
und 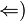 . Formulieren Sie beide Aussagen so, dass sie auch Schüler einer neunten Klasse Werkrealschule verstehen können.
. Formulieren Sie beide Aussagen so, dass sie auch Schüler einer neunten Klasse Werkrealschule verstehen können.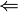 mittels eines Widerspruchsbeweises.
mittels eines Widerspruchsbeweises. im Punkt
im Punkt 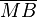 .
.
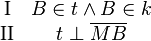
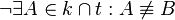
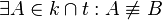
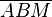 ist gleichschenklig, weil
ist gleichschenklig, weil 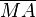 und
und 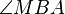 und
und 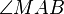 sind die Basiwinkel dieses Dreiecks. Weil nach
sind die Basiwinkel dieses Dreiecks. Weil nach  der Winkel
der Winkel 
