Lösung von Aufgabe 3.4 (WS 11/12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Beweisen Sie auf der Grundlage der Definition aus Aufgabe 3.3:<br /> Die Winkelhalbierende eines Winkels ist die Menge aller Punkte, die im Inneren des Winkels li…“)
 
Zeile 5: Zeile 5:
 
*Der Beweis geht in zwei Schritten: Sie müssen erstens zeigen, dass jeder Punkt der Winkelhalbierenden (entspr. Def. Aufg. 3.3) von den beiden Schenkeln den gleichen Abstand hat und zweitens, dass jeder Punkt, der von den beiden Schenkeln den gleichen Abstand hat und im Inneren des Winkels liegt, zur Winkelhalbierenden (entspr. Def. Aufg. 3.3) gehört.
 
*Der Beweis geht in zwei Schritten: Sie müssen erstens zeigen, dass jeder Punkt der Winkelhalbierenden (entspr. Def. Aufg. 3.3) von den beiden Schenkeln den gleichen Abstand hat und zweitens, dass jeder Punkt, der von den beiden Schenkeln den gleichen Abstand hat und im Inneren des Winkels liegt, zur Winkelhalbierenden (entspr. Def. Aufg. 3.3) gehört.
 
*Die Beweise lassen sich mit Hilfe der Kongruenzsätze führen, die Sie aus der Schule bereits kennen sollten.
 
*Die Beweise lassen sich mit Hilfe der Kongruenzsätze führen, die Sie aus der Schule bereits kennen sollten.
 +
 +
 +
[[Bild:PaufWhalb.png‎|200px]]
 +
 +
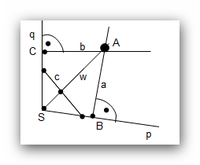
Voraussetzung:
 +
 +
<math>\angle w,p = \angle w,q</math>
 +
 +
<math>\angle p,a = \angle q,b</math> = 90°
 +
 +
<math>\overline{SA} = \overline{,SA}</math>
 +
 +
Behauptung1:
 +
 +
<math>a \tilde {=} b</math>
 +
 +
Beweis:
 +
<math>\angle p,c = \angle c,q  \wedge \angle p,a  = \angle b,q  \wedge \overline{AS} = \overline{AS \Rightarrow } Dreieck \overline{SAB} \tilde {=} Dreieck\overline{SCA} \Rightarrow a \tilde {=} b</math> Kongruenzsatz WSW
 +
 +
Behauptung2:
 +
 +
<math>\forall A :\left| Ap \right| = \left| Aq \right| \Leftrightarrow A\in w</math>
 +
 +
--[[Benutzer:RicRic|RicRic]]
 +
 +
 +
  
  
 
[[Category:Einführung_Geometrie]]
 
[[Category:Einführung_Geometrie]]

Version vom 30. Oktober 2011, 15:08 Uhr

Beweisen Sie auf der Grundlage der Definition aus Aufgabe 3.3:
Die Winkelhalbierende eines Winkels ist die Menge aller Punkte, die im Inneren des Winkels liegen und deren Abstände von den beiden Schenkeln des Winkels jeweils gleich sind.
Anmerkung:

  • Der Abstand eines Punktes P auf eine Gerade g ist die Länge des Lotes von P auf g.
  • Der Beweis geht in zwei Schritten: Sie müssen erstens zeigen, dass jeder Punkt der Winkelhalbierenden (entspr. Def. Aufg. 3.3) von den beiden Schenkeln den gleichen Abstand hat und zweitens, dass jeder Punkt, der von den beiden Schenkeln den gleichen Abstand hat und im Inneren des Winkels liegt, zur Winkelhalbierenden (entspr. Def. Aufg. 3.3) gehört.
  • Die Beweise lassen sich mit Hilfe der Kongruenzsätze führen, die Sie aus der Schule bereits kennen sollten.


PaufWhalb.png

Voraussetzung:

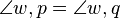
\angle w,p = \angle w,q

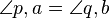\angle p,a = \angle q,b = 90°

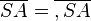
\overline{SA} = \overline{,SA}

Behauptung1:

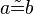
a \tilde {=} b

Beweis: 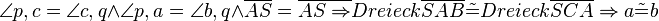\angle p,c = \angle c,q \wedge \angle p,a = \angle b,q \wedge \overline{AS} = \overline{AS \Rightarrow } Dreieck \overline{SAB} \tilde {=} Dreieck\overline{SCA} \Rightarrow a \tilde {=} b Kongruenzsatz WSW

Behauptung2:

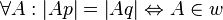
\forall A :\left| Ap \right| = \left| Aq \right| \Leftrightarrow A\in w

--RicRic

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_3.4_(WS_11/12)&oldid=9076“