Lösung von Aufgabe 4.3 S (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 4.3)
(→‎Aufgabe 4.3)
Zeile 16: Zeile 16:
 
'''Lösungsvorschlag 1:'''
 
'''Lösungsvorschlag 1:'''
  
−
1.) „Wenn <math>A</math>,<math>B</math> und <math>C</math> nicht kollinear sind, dann sind sie paarweise verschieden.“
+
'''1)''' „Wenn <math>A</math>,<math>B</math> und <math>C</math> nicht kollinear sind, dann sind sie paarweise verschieden.“
  
−
2.)<br />Voraussetzung: nkoll (A,B,C)<br />Behauptung: A,B und C sind paarweise verschieden<br />Annahme: 2 Punkte sind nicht paarweise verschieden (Widerspruch zur Behauptung..)
+
'''2)'''<br />Voraussetzung: nkoll (A,B,C)<br />Behauptung: A,B und C sind paarweise verschieden<br />Annahme: 2 Punkte sind nicht paarweise verschieden (Widerspruch zur Behauptung..)
  
 
{| class="wikitable sortable"  
 
{| class="wikitable sortable"  
Zeile 29: Zeile 29:
 
| (3) || <math>\exists g:g=AC</math> || (2), Axiom I/1
 
| (3) || <math>\exists g:g=AC</math> || (2), Axiom I/1
 
|-  
 
|-  
−
| (4) || <math>\operatorname{koll}(A, B, C)</math>  || (3), Def. kollinear
+
| (4) || <math>\operatorname{koll}(A, B, C)</math>  || (2), (3), Def. kollinear
 
|-  
 
|-  
 
| (5) || Widerspruch zur Voraussetzung || (4), (1)
 
| (5) || Widerspruch zur Voraussetzung || (4), (1)
Zeile 38: Zeile 38:
  
  
−
3.) „Wenn <math>A</math>,<math>B</math> und <math>C</math> nicht paarweise verschieden sind, dann sind sie kollinear.“
+
'''3)''' „Wenn <math>A</math>,<math>B</math> und <math>C</math> nicht paarweise verschieden sind, dann sind sie kollinear.“
  
−
5.) „Wenn <math>A</math>,<math>B</math> und <math>C</math> paarweise verschieden sind, dann sind sie nicht kollinear.“ --[[Benutzer:Nummero6|Tchu Tcha Tcha]] 15:39, 13. Mai 2012 (CEST)
+
'''4)'''<br />Voraussetzung: mindestens 2 der 3 Punkte (A,B,C) sind identisch<br />Behauptung: koll (A,B,C)<br />
 +
 
 +
{| class="wikitable sortable"
 +
!!!Beweisschritt!!Begründung
 +
|-
 +
| (1) || oBdA: <math>A=B ; A \neq C </math> || Voraussetzung
 +
|-
 +
| (2) || <math>\exists g:g=AC</math> || (1), Axiom I/1
 +
|-
 +
| (3) || <math>\operatorname{koll}(A, B, C)</math>  || (1), (2), Def. kollinear
 +
|-
 +
|}
 +
 
 +
 
 +
'''5)''' „Wenn <math>A</math>,<math>B</math> und <math>C</math> paarweise verschieden sind, dann sind sie nicht kollinear.“
 +
 
 +
'''6)''' Die Umkehrung von Satz I gilt NICHT!!! (siehe Gegenbeispiel)
 +
 
 +
<ggb_applet width="531" height="441"  version="4.0" ggbBase64="UEsDBBQACAAIAHOZrUAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAHOZrUAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1Vhtj9NGEP4Mv2LkzyTZd9soAQESKtJBkY5WVb9t7L1kOcd27U0uh/jxnd21c8ndcVBAVYsI+zKzMzsvz8ya+fP9poKd6Xrb1IuETkkCpi6a0tarRbJ1F5Msef7s8XxlmpVZdhoumm6j3SIRntOWi+RCsswYJialTJcTwUoxyYkoJkwXS6NzQjUpEoB9b5/WzTu9MX2rC3NerM1GnzWFdkHx2rn26Wx2dXU1HVVNm241W62W031fJoDXrPtFMkyeoriTQ1c8sDNC6OyPt2dR/MTWvdN1YRLwJmzts8eP5le2LpsruLKlWy8SyWkCa2NXa7RJSlzMPFOLDmlN4ezO9Hj0aBlsdps2CWy69vRHcQbVwZwESruzpekWCZnyVCmRZlywVOSS5Qk0nTW1G3hHnbNR2nxnzVUU62dBo0jANU211F4ifP4MjDACT/xA48BwUCqSSNwjPA4sDiIOMvKIeFxEVhF5ROQRPIGd7e2yMhhgXfXoQVtfdBi9w7p315UJ9xk2bqynT9Cm3n5CZk4wTaLLcZ+QJ/6n8Cc8YXZqJD3S6rrtP1Q6qgwh/VaV7IcM5aNOdp+ZTH7BTPWA0mj3t9hJ5ZFOVBX+ht8djfwhM29rjOsfU6jEv2LifDZCZT6gA/q15x2yx5lN7/HCc5C5T3sKErGhUsxyCTTHIWWAaAAqQUhc0gyUH1PgKRIEcMjA81EOARwyw39EGoQpkCjM76aISaCoSIDkQAOmBCCSIOASMco4ckgJEg959ZR5EVyBULjiGQi8o4dkSpGR40Fco3oGnAL3h2kKTIHy8qjwUFeZvzqKZKAIKOoFIqoR0RHNyJ8B99aowV22brfuxEXFphynrmkPsUBurEc3VS/Wp5Oi+Ghe6aWpsE+c+0gC7HTlEREUXTS1gzGILO6tOt2ubdGfG+fwVA8f9U6faWf2r5G7H3UH3qKp+/dd41411XZT9wBFU5HDnZuKHs3Z4da44EcEcUyQRwR1NE/v1dsgBba9Qf1N14/suizfeI6b0oCe/LWurl92Rl+2jT01Yz4LLWdutkVlS6vr3zFZvRbvF7i3AwnKx4s0XXl+3WMGw/5P0zXoxzSfqjzFbpKliACs7glcR5IgairyVKU5DyRflwrtsZeqaU5UJuI+9gA8c4ckcv9HRM1mdwiQ3psbW1edPaSKn7/pXzZVeSAH61/p1m278HTAK3Tephf1qjIhQ0Kxxb5cXC6b/XlMDR5lfbhucUXiBZar4HXAysCkRIZhXMYx8PibHbhI4CGBg4y5ZssDneYscIRxGcfAhckbrzZYSkcrKRnV2D7UM5IMqBlrlU993+a3tXVn48LZ4nIwlcYD77abpTkk0KlM+rNkzme3Mmx+abraVENCYyy3zbaP+DzK9dIUdoPLSBhcon24fsMLxN3SrDozXrwKz7LosEAlx7l6ZzuIet01mzf17gPmwq0LzGfjLed90dnWpxwssQlcmpusKm2vsYeUx+c8AtH0wvcKdI/zrkFsbt266cLLC0sKjh54ldngOwtcSK+QoQc3vwgPOO9PaJYfsaodGl+k3wQMyfemWkhKXbVr7R95g9GVvjbdiRuCvLdNeds56PtgAUK8jbFtjYlpEe+LkxbFBTSdlCj0dg/7RTIhWA8yRjkTgmYZloUM0Y0XmxKSZVgKUsp4plSawKf4tI9vW+8Hj7+Tih13bwURMyu68CvOfPn/dyad5hnhkhGq0kxJgV0r+pJnEosuFyqjLJO+tP4EZxbNZqPrEurwIDrDOpTc9GdNfHqCpt6x0WtbNxJ0FDUIuBMXX9IObtdfCcuRI74UF/L9UTlJVExGkuYylTLFXOVUDt5FZ0slmSJ5Kpn/NELnTuRUCcG4xI8aQTIu1e1y7fAdcYkfS33oKW7oHmHyiy1LE96QsZv9VccjfayhdtNWtrDu4YC8D9l9GhF9JxSvHg7FKURefRdEKIsNMIz/BZjwqcSPRIrRzKXC8DAxBhI/LJlimaBCIozkT4HJ7LjWhwfV8H8Dz/4GUEsHCNCiwEzoBQAAuBAAAFBLAQIUABQACAAIAHOZrUDWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAc5mtQNCiwEzoBQAAuBAAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAB/BgAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />
 +
 
 +
--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 19:12, 13. Mai 2012 (CEST)

Version vom 13. Mai 2012, 19:12 Uhr

Aufgabe 4.3

Satz I: Je drei nicht kollineare Punkte sind paarweise verschieden.

  1. Wir formulieren Satz I neu und beginnen mit „Es seien A, B und C drei Punkte.“ Ergänzen Sie: „Wenn A,B und C … , dann … .“
  2. Beweisen Sie Satz I indirekt mit Widerspruch.
  3. Bilden Sie die Kontraposition von Satz I.
  4. Beweisen Sie auch die Kontraposition von Satz I.
  5. Formulieren Sie die Umkehrung von Satz I.
  6. Gilt auch die Umkehrung von Satz I?



Lösungsvorschlag 1:

1) „Wenn A,B und C nicht kollinear sind, dann sind sie paarweise verschieden.“

2)
Voraussetzung: nkoll (A,B,C)
Behauptung: A,B und C sind paarweise verschieden
Annahme: 2 Punkte sind nicht paarweise verschieden (Widerspruch zur Behauptung..)

Beweisschritt Begründung
(1) 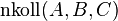\operatorname{nkoll}(A, B, C) Voraussetzung
(2) oBdA: 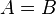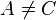A=B ; A \neq C Annahme
(3) 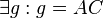\exists g:g=AC (2), Axiom I/1
(4) 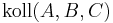\operatorname{koll}(A, B, C) (2), (3), Def. kollinear
(5) Widerspruch zur Voraussetzung (4), (1)
(6) Behauptung stimmt (5)


3) „Wenn A,B und C nicht paarweise verschieden sind, dann sind sie kollinear.“

4)
Voraussetzung: mindestens 2 der 3 Punkte (A,B,C) sind identisch
Behauptung: koll (A,B,C)

Beweisschritt Begründung
(1) oBdA: 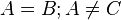A=B ; A \neq C Voraussetzung
(2) 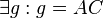\exists g:g=AC (1), Axiom I/1
(3) 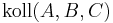\operatorname{koll}(A, B, C) (1), (2), Def. kollinear


5) „Wenn A,B und C paarweise verschieden sind, dann sind sie nicht kollinear.“

6) Die Umkehrung von Satz I gilt NICHT!!! (siehe Gegenbeispiel) 

--Tchu Tcha Tcha 19:12, 13. Mai 2012 (CEST)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_4.3_S_(SoSe_12)&oldid=13251“