Lösung von Aufgabe 6.3 S (SoSe 12): Unterschied zwischen den Versionen
(→Anmerkungen von Buchner) |
Snooth (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| − | |||
== Aufgabe 6.3 == | == Aufgabe 6.3 == | ||
Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt.<br /> | Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt.<br /> | ||
| Zeile 30: | Zeile 29: | ||
In Schritt zwei wirds jetzt unsauber. Nach Annahme ist N eine weiterer, von M verschiedener Mittelpunkt. Nach Definition für Mittelpunkt gilt: <math>N \in \overline{AB}</math> und <math>\left| AN \right| = \left| NB \right| </math>. Dass <math>\left| AN \right| =\frac{\left| AB \right|}{2}</math> ist, müssen Sie noch zeigen (Sie dürfen das also nicht einfach annhemen) . Hier fehlen ein, zwei Zwischenschritte. Ansonsten schon wirklich gut!<br /> | In Schritt zwei wirds jetzt unsauber. Nach Annahme ist N eine weiterer, von M verschiedener Mittelpunkt. Nach Definition für Mittelpunkt gilt: <math>N \in \overline{AB}</math> und <math>\left| AN \right| = \left| NB \right| </math>. Dass <math>\left| AN \right| =\frac{\left| AB \right|}{2}</math> ist, müssen Sie noch zeigen (Sie dürfen das also nicht einfach annhemen) . Hier fehlen ein, zwei Zwischenschritte. Ansonsten schon wirklich gut!<br /> | ||
--[[Benutzer:Buchner|Buchner]] 12:11, 6. Jun. 2012 (CEST) | --[[Benutzer:Buchner|Buchner]] 12:11, 6. Jun. 2012 (CEST) | ||
| + | |||
| + | ''in progress'' | ||
| + | === Noch ein Versuch: === | ||
| + | |||
| + | :<u>Def. (Mittelpunkt einer Strecke):</u> | ||
| + | Wenn ein Punkt <math>M</math> einer Strecke <math> \overline {AB} </math> zu den beiden Endpunkten <math>A</math> und <math>B</math><br /> jeweils ein und denselben Abstand hat, heißt <math>M</math> der Mittelpunkt der Strecke <math> \overline {AB} </math>. | ||
| + | |||
| + | was nun zu zeigen wäre:<br /> ''Jede Strecke hat höcstens einen Mittelpunkt.'' | ||
| + | |||
| + | --[[Benutzer:Snooth|Snooth]] 13:14, 16. Jun. 2012 (CEST) | ||
Version vom 16. Juni 2012, 13:14 Uhr
Inhaltsverzeichnis |
Aufgabe 6.3
Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt.
--H2O 20:07, 28. Mai 2012 (CEST) und keinKurpfälzer
Anmerkungen von Buchner
Leider kann ich das eingescannte Dokument nicht so gut lesen unten.
Zu Ihrem ersten Beweisversuch. Die Annahme und die ersten Schritte sind gut. Ab Schritt 5 macht der Beweis für mich aber keinen Sinn. Rechnen Sie doch mal mit den Gleichungen aus Schritt 3 und 4 weiter!
Kleiner Tipp: Der Widerspruch sollte was mit dem Axiom vom Lineal zu tun haben!--Buchner 16:18, 31. Mai 2012 (CEST)
Ich kann leider immer noch nicht diese Zeichen einfügen, deswegen ist meine Lösung ohne Formeln^^
Vorraussetzung: Strecke AB mit Mittelpunkt M
Behauptung: Es gibt keinen weiteren Mittelpunkt N, der nicht zu M identisch ist
Annahme: Es gibt noch weitere Mittelpunkte N, die nicht zu M identisch sind
Beweis:
(1) Es gibt ein M, das auf AB liegt und zu A den Abstand AM hat, dieser Abstand ist gleich MB, also AB/2 | Vor., Def. Mittelp.
(2) Es gibt einen weiteren Punkt N ungleich M, der ebenfalls auf AB liegt und von A den Abstand AB/2 hat | Beh., Def. Mittelp.
Widerspruch zum Axiom vom Lineal (denn es gibt nur genau einen Punkt mit Abstand x zu A)
--Monsta 13:15, 5. Jun. 2012 (CEST)
Anmerkungen von Buchner zu Monstas Beweis
Das sieht schon sehr gut aus!
Vor, Beh und Ann sind absolut korrekt.
Schritt eins ist auch in Ordnung- ergänzen Sie noch in der Begründung, dass Sie sich auf den Existenzbeweis beziehen. (Die Definition sagt nämlich noch nicht aus, dass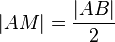 
, aber das wissen wir aus dem Existenzbeweis.)
In Schritt zwei wirds jetzt unsauber. Nach Annahme ist N eine weiterer, von M verschiedener Mittelpunkt. Nach Definition für Mittelpunkt gilt: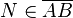 
und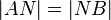 
. Dass 
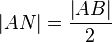ist, müssen Sie noch zeigen (Sie dürfen das also nicht einfach annhemen) . Hier fehlen ein, zwei Zwischenschritte. Ansonsten schon wirklich gut!
--Buchner 12:11, 6. Jun. 2012 (CEST)
in progress
Noch ein Versuch:
- Def. (Mittelpunkt einer Strecke):
Wenn ein Punkteiner Strecke
zu den beiden Endpunkten
und
jeweils ein und denselben Abstand hat, heißt
was nun zu zeigen wäre:
Jede Strecke hat höcstens einen Mittelpunkt.
--Snooth 13:14, 16. Jun. 2012 (CEST)
