Lösung von Aufgabe 8.1
Aus Geometrie-Wiki
Version vom 21. Juli 2010, 09:25 Uhr von Barbarossa (Diskussion | Beiträge)
Es sei  eine Ebene, die durch die Gerade
eine Ebene, die durch die Gerade  in die beiden Halbebenen
in die beiden Halbebenen 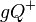 und
und 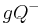 eingeteilt wird. Ferner sei
eingeteilt wird. Ferner sei 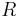 ein Punkt der Halbebene
ein Punkt der Halbebene 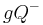 , der nicht auf der Trägergeraden
, der nicht auf der Trägergeraden  liegen möge.
Beweisen Sie:
liegen möge.
Beweisen Sie:  und
und 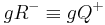
Lösung --Schnirch 13:10, 14. Jul. 2010 (UTC)
Voraussetzung: 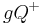 und
und 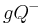
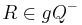 mit
mit 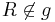
Behauptung:  und
und 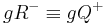 , d. h.
, d. h.
1) 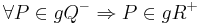
2) 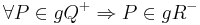
zu 1)
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 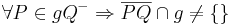
|
nach Definition Halbebene |
| (II) | 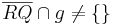
|
nach Voraussetzung und Definition Halbebene |
| (III) | 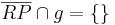
|
Axiom v. Pasch |
| (IV) | 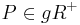
|
(III) und Definition Halbebene |
zu 2) analog zu 1)
Aber hier wurde doch wie in der ersten Version des Wiki-Kapitels zu den Halbebenen nicht beachtet, dass auch koll (P, R, Q) gelten könnte. Müsste man diese Fallunterscheidung nicht noch machen??? --Barbarossa 07:25, 21. Jul. 2010 (UTC)

