Lösung von Zusatzaufgabe 6.1 S (SoSe 12): Unterschied zwischen den Versionen
(→Bemerkungen M.G.) |
|||
| (16 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | |||
| − | |||
=== Zusatzaufgabe 6.1 === | === Zusatzaufgabe 6.1 === | ||
Es sei <math>\ g</math> eine Gerade und <math>\ P</math> ein Punkt, der nicht zu <math>\ g</math> gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene <math>\ \varepsilon</math>, die sowohl alle Punkte von <math>\ g</math> als auch den Punkt <math>\ P</math> enthält.<br /> | Es sei <math>\ g</math> eine Gerade und <math>\ P</math> ein Punkt, der nicht zu <math>\ g</math> gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene <math>\ \varepsilon</math>, die sowohl alle Punkte von <math>\ g</math> als auch den Punkt <math>\ P</math> enthält.<br /> | ||
| − | + | ===Lösungsvorschlag von Quadratisch , Praktisch, Gut=== | |
| − | Voraussetzung: Gerade g, Punkt P, P nicht Element von g | + | Voraussetzung: Gerade g, Punkt P, P nicht Element von g<br/> |
| − | {| class="wikitable | + | Behauptung: Es existiert eine Ebene, die sowohl g als auch P enthält. |
| + | {| class="wikitable" | ||
!Schritt!!Warum darf ich den Schritt machen? | !Schritt!!Warum darf ich den Schritt machen? | ||
|- | |- | ||
| − | | Es existiert X,Y.X,Y Element g || I.2 | + | | (1)Es existiert X,Y.X,Y Element g || I.2 |
|- | |- | ||
| − | | nkoll(X,Y,P) || (1), Vor. | + | | (2)nkoll(X,Y,P) || (1), Vor. |
|- | |- | ||
| − | | Es existiert eine Ebene.X,Y,P Element der Ebene || (2), I.4 | + | | (3)Es existiert eine Ebene.X,Y,P Element der Ebene || (2), I.4 |
|} | |} | ||
Durch Axiom I.4 wären Existenz ('''Zu drei nicht kollinearen Punkten gibt es''' genau '''eine Ebene'''...) und Eindeutigkeit (... '''genau eine Ebene'''...) bewiesen. <br/> | Durch Axiom I.4 wären Existenz ('''Zu drei nicht kollinearen Punkten gibt es''' genau '''eine Ebene'''...) und Eindeutigkeit (... '''genau eine Ebene'''...) bewiesen. <br/> | ||
--[[Benutzer:RitterSport|RitterSport]] 20:02, 4. Jun. 2012 (CEST) | --[[Benutzer:RitterSport|RitterSport]] 20:02, 4. Jun. 2012 (CEST) | ||
| + | ===Bemerkungen M.G.=== | ||
| + | Der Beweis ist soweit korrekt aber noch nicht ganz vollständig. Das Axiom I/4 sichert uns nur, dass Ihre Punkte <math>X,Y,P</math> in der Ebene <math>\varepsilon</math> liegen. Wir sollen aber zeigen, dass alle Punkte der Geraden <math>g</math> in <math>\varepsilon</math> liegen. | ||
| + | |||
| + | Hier noch mal Ihr Beweis mit LaTex Tags. Schritt 4 wäre noch zu ergänzen.(Meine Begründungen fallen etwas ausführlicher aus, weil viele Leser sicherlich die Axiome nicht im Kopf haben.) | ||
| + | |||
| + | {| class="wikitable" | ||
| + | !Nr. !!Schritt !! Warum darf ich den Schritt machen? | ||
| + | |- | ||
| + | | (1) || <math>\exist X, Y : X \in g \wedge Y \in g</math> || Axiom I/2: Auf jeder Geraden gibt es zwei verschiedene Punkte. | ||
| + | |- | ||
| + | | (2) ||<math>\operatorname{nkoll} (X,Y,P)</math>||Nach Voraussetzung gehört <math>P</math> nicht zu <math>g</math>, was nach Schritt 1 für die beiden Punkte <math>X</math> und <math>Y</math> jedoch zutrifft. | ||
| + | |- | ||
| + | | (3)|| <math>\exist \varepsilon: X, Y, P \in \varepsilon</math> || Axiom I/4: Zu je drei nichtkollinearen Punkten gibt es genau eine Ebene, zu der die drei Punkte gehören. | ||
| + | |- | ||
| + | | (4)|| <math>g \subset \varepsilon</math> || Axiom ... | ||
| + | |} | ||
| + | <br /> | ||
| + | Bei Schritt (4) würde ich als Begründung das Axiom I.5 anwenden, welches besagt, dass "wenn 2 Punkte einer Geraden g in einer Ebene E liegen, so gehört g zu E". <br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 13:47, 9. Jul. 2012 (CEST)<br /> | ||
| + | *Ja, dann passt der Beweis auch so. --[[Benutzer:Andreas|Tutor Andreas]] 11:32, 12. Jul. 2012 (CEST) | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
Aktuelle Version vom 12. Juli 2012, 11:32 Uhr
Zusatzaufgabe 6.1
Es sei  eine Gerade und
eine Gerade und  ein Punkt, der nicht zu
ein Punkt, der nicht zu  gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene
gehört. Beweisen Sie mittels der Axiome der Inzidenz: Es gibt genau eine Ebene  , die sowohl alle Punkte von
, die sowohl alle Punkte von  als auch den Punkt
als auch den Punkt  enthält.
enthält.
Lösungsvorschlag von Quadratisch , Praktisch, Gut
Voraussetzung: Gerade g, Punkt P, P nicht Element von g
Behauptung: Es existiert eine Ebene, die sowohl g als auch P enthält.
| Schritt | Warum darf ich den Schritt machen? |
|---|---|
| (1)Es existiert X,Y.X,Y Element g | I.2 |
| (2)nkoll(X,Y,P) | (1), Vor. |
| (3)Es existiert eine Ebene.X,Y,P Element der Ebene | (2), I.4 |
Durch Axiom I.4 wären Existenz (Zu drei nicht kollinearen Punkten gibt es genau eine Ebene...) und Eindeutigkeit (... genau eine Ebene...) bewiesen.
--RitterSport 20:02, 4. Jun. 2012 (CEST)
Bemerkungen M.G.
Der Beweis ist soweit korrekt aber noch nicht ganz vollständig. Das Axiom I/4 sichert uns nur, dass Ihre Punkte 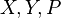 in der Ebene
in der Ebene  liegen. Wir sollen aber zeigen, dass alle Punkte der Geraden
liegen. Wir sollen aber zeigen, dass alle Punkte der Geraden  in
in  liegen.
liegen.
Hier noch mal Ihr Beweis mit LaTex Tags. Schritt 4 wäre noch zu ergänzen.(Meine Begründungen fallen etwas ausführlicher aus, weil viele Leser sicherlich die Axiome nicht im Kopf haben.)
| Nr. | Schritt | Warum darf ich den Schritt machen? |
|---|---|---|
| (1) | 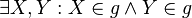 |
Axiom I/2: Auf jeder Geraden gibt es zwei verschiedene Punkte. |
| (2) | 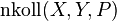 |
Nach Voraussetzung gehört  nicht zu nicht zu  , was nach Schritt 1 für die beiden Punkte , was nach Schritt 1 für die beiden Punkte 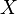 und und 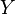 jedoch zutrifft. jedoch zutrifft.
|
| (3) | 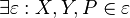 |
Axiom I/4: Zu je drei nichtkollinearen Punkten gibt es genau eine Ebene, zu der die drei Punkte gehören. |
| (4) | 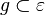 |
Axiom ... |
Bei Schritt (4) würde ich als Begründung das Axiom I.5 anwenden, welches besagt, dass "wenn 2 Punkte einer Geraden g in einer Ebene E liegen, so gehört g zu E".
--Tchu Tcha Tcha 13:47, 9. Jul. 2012 (CEST)
- Ja, dann passt der Beweis auch so. --Tutor Andreas 11:32, 12. Jul. 2012 (CEST)

