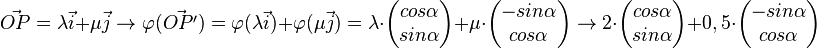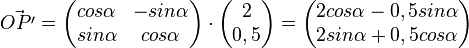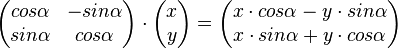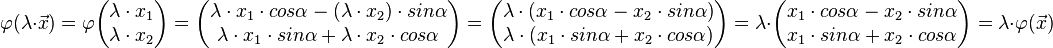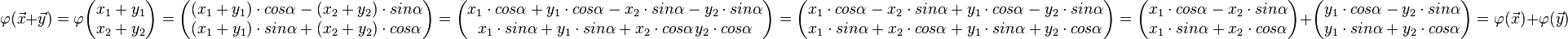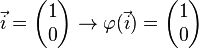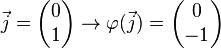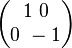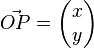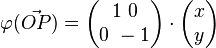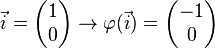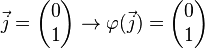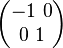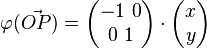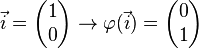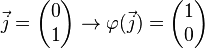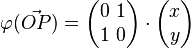Lineare Abbildungen, Vektorraumisomorphismus 2012 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Definition) |
Jessy* (Diskussion | Beiträge) (→Spiegelung an der 1. Winkelhalbierenden:) |
||
| (31 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
=Definition= | =Definition= | ||
| − | {{Definition|(lineare Abbildung)<br />Es seien <math>\left(V_1, \oplus, \mathbb{R}, \cdot\right)</math> und <math>\left(V_2, \otimes, \mathbb{R}, \odot\right)</math> zwei Vektorräume über der Körper der reellen Zahlen. <br />Eine Abbildung <math>\varphi: V_1 \rightarrow V_2</math> heißt lineare Abbildung wenn gilt: <br /><math>\forall \vec{u}, \vec{v} \in V_1 \wedge \forall a \in \mathbb{R}:</math> <br /> | + | {{Definition|(lineare Abbildung)<br />Es seien <math>\left(V_1, \oplus, \mathbb{R}, \cdot\right)</math> und <math>\left(V_2, \otimes, \mathbb{R}, \odot\right)</math> zwei Vektorräume über der Körper der reellen Zahlen. <br />Eine Abbildung <math>\varphi: V_1 \rightarrow V_2</math> heißt lineare Abbildung wenn gilt: <br /><math>\forall \vec{u}, \vec{v} \in V_1 \wedge \forall a \in \mathbb{R}:</math> <br />(H) <math>\varphi</math> ist homogen: <math>\varphi\left(a \cdot \vec{u} \right) = a \odot \varphi\left(\vec{u}\right)</math><br />(A) <math>\varphi</math> ist additiv: <math>\varphi\left(\vec{u} \oplus \vec{v} \right)= \varphi \left(\vec{u}\right) \otimes \varphi \left(\vec{v}\right)</math> }} |
| + | =Beispiele= | ||
| + | ==senkrechte Parallelprojektion auf die x-y-Ebene== | ||
| + | <math>\varphi: \mathbb{R}^3 \rightarrow \mathbb{R}^2</math><br /> | ||
| + | <math>\forall \begin{pmatrix} x \\ y \\ z \end{pmatrix}: \varphi \left( \begin{pmatrix} x \\ y \\ z \end{pmatrix}\right)= \begin{pmatrix} x \\ y \end{pmatrix}</math><br /> | ||
| + | Man beweise: <math>\varphi</math> ist lineare Abbildung<br /><br /> | ||
| + | ==Drehung== | ||
| + | <u>''' | ||
| + | ==== Drehungen um den Ursprung des Koordinatensystems ==== | ||
| + | ''' | ||
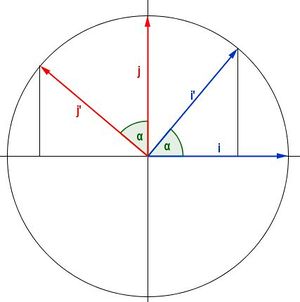
| + | Drehung der kanonischen Basisvektoren</u><br /> | ||
| + | <math> \vec{i} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \rightarrow \varphi( \vec{i}) = \begin{pmatrix} cos \alpha \\ sin \alpha \end{pmatrix}</math><br /><br /> | ||
| + | <math> \vec{j} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \rightarrow \varphi( \vec{j}) =\begin{pmatrix} -sin \alpha \\ cos \alpha \end{pmatrix}</math><br /><br /> | ||
| + | [[Bild:Drehung_kanonische_Basis.JPG|300px]]<br /><br /> | ||
| + | <u>Drehung anderer Vektoren:</u><br /> | ||
| + | <math> \vec{x} \rightarrow \varphi( \vec{x} )</math><br /><br /> | ||
| + | <math> \vec{x} = \lambda \vec{i} + \mu \vec{j} \rightarrow \varphi( \vec{x}) = \varphi ( \lambda \vec{i}) + \varphi( \mu \vec{j}) = \lambda \cdot \begin{pmatrix} cos \alpha \\ sin \alpha \end{pmatrix} + \mu \cdot \begin{pmatrix} -sin \alpha \\ cos \alpha \end{pmatrix}</math><br /><br /> | ||
| + | Bsp.: <math> \vec{OP} = \begin{pmatrix} 2 \\ 0,5 \end{pmatrix} </math> wird an O um <math> \alpha </math> gedreht.<br /> | ||
| + | <math> \vec{OP} = \lambda \vec{i} + \mu \vec{j} \rightarrow \varphi( \vec{OP'}) = \varphi ( \lambda \vec{i}) + \varphi( \mu \vec{j}) = \lambda \cdot \begin{pmatrix} cos \alpha \\ sin \alpha \end{pmatrix} + \mu \cdot \begin{pmatrix} -sin \alpha \\ cos \alpha \end{pmatrix} \rightarrow 2 \cdot \begin{pmatrix} cos \alpha \\ sin \alpha \end{pmatrix} + 0,5 \cdot \begin{pmatrix} -sin \alpha \\ cos \alpha \end{pmatrix}</math><br /><br /> | ||
| + | <math> \vec{OP'} = \begin{pmatrix} cos \alpha & -sin \alpha\\ sin \alpha & cos \alpha \end{pmatrix} \cdot \begin{pmatrix} 2 \\ 0,5 \end{pmatrix} = \begin{pmatrix} 2cos \alpha -0,5sin \alpha\\ 2sin \alpha + 0,5cos \alpha \end{pmatrix}</math><br /><br /> | ||
| + | <u>Drehungsmatrix:</u><br /> | ||
| + | <math>\begin{pmatrix} cos \alpha & -sin \alpha\\ sin \alpha & cos \alpha \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} x \cdot cos \alpha -y \cdot sin \alpha\\ x \cdot sin \alpha + y \cdot cos \alpha \end{pmatrix}</math><br /><br /> | ||
| + | ==== Drehung um den Ursprung des Koordinatensystems als lineare Abbildung: ==== | ||
| + | Behauptung: <math> \varphi </math> ist eine lineare Abbildung.<br /><br /> | ||
| + | Zu zeigen:<br /> | ||
| + | (H) <math> \varphi </math> ist homogen<br /> | ||
| + | (A) <math> \varphi </math> ist additiv<br /><br /> | ||
| + | Beweis zur Homogenität:<br /> | ||
| + | <math> \varphi ( \lambda \cdot \vec{x}) = | ||
| + | \varphi \begin{pmatrix} \lambda \cdot x_1 \\ \lambda \cdot x_2 \end{pmatrix}= | ||
| + | \begin{pmatrix} \lambda \cdot x_1 \cdot cos \alpha -( \lambda \cdot x_2) \cdot sin \alpha\\ \lambda \cdot x_1 \cdot sin \alpha + \lambda \cdot x_2 \cdot cos \alpha \end{pmatrix} = | ||
| + | \begin{pmatrix} \lambda \cdot (x_1 \cdot cos \alpha - x_2 \cdot sin \alpha) \\ \lambda \cdot (x_1 \cdot sin \alpha + x_2 \cdot cos \alpha) \end{pmatrix} = | ||
| + | \lambda \cdot \begin{pmatrix} x_1 \cdot cos \alpha - x_2 \cdot sin \alpha \\ x_1 \cdot sin \alpha + x_2 \cdot cos \alpha \end{pmatrix} = | ||
| + | \lambda \cdot \varphi ( \vec{x}) | ||
| + | </math><br /><br /> | ||
| + | Beweis zur Additivität:<br /> | ||
| + | <math> \varphi ( \vec{x} + \vec{y}) = | ||
| + | \varphi \begin{pmatrix} x_1+y_1 \\ x_2+y_2 \end{pmatrix} = | ||
| + | \begin{pmatrix} (x_1+y_1) \cdot cos \alpha -(x_2+y_2) \cdot sin \alpha\\ (x_1+y_1) \cdot sin \alpha + (x_2+y_2) \cdot cos \alpha \end{pmatrix} = | ||
| + | \begin{pmatrix} x_1 \cdot cos \alpha + y_1 \cdot cos \alpha -x_2 \cdot sin \alpha - y_2 \cdot sin \alpha\\ x_1 \cdot sin \alpha + y_1 \cdot sin \alpha + x_2 \cdot cos \alpha y_2 \cdot cos \alpha \end{pmatrix} = | ||
| + | \begin{pmatrix} x_1 \cdot cos \alpha -x_2 \cdot sin \alpha + y_1 \cdot cos \alpha - y_2 \cdot sin \alpha\\ x_1 \cdot sin \alpha + x_2 \cdot cos \alpha + y_1 \cdot sin \alpha + y_2 \cdot cos \alpha \end{pmatrix} = | ||
| + | \begin{pmatrix} x_1 \cdot cos \alpha -x_2 \cdot sin \alpha \\ x_1 \cdot sin \alpha + x_2 \cdot cos \alpha \end{pmatrix} + | ||
| + | \begin{pmatrix} y_1 \cdot cos \alpha - y_2 \cdot sin \alpha \\ y_1 \cdot sin \alpha + y_2 \cdot cos \alpha \end{pmatrix} = | ||
| + | \varphi ( \vec{x}) + \varphi ( \vec{y})</math> | ||
| + | ==Geradenspiegelung== | ||
| + | ==== Spiegelung an der x-Achse: ==== | ||
| + | <math> \vec{i} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \rightarrow \varphi( \vec{i}) = \begin{pmatrix} 1 \\ 0 \end{pmatrix}</math><br /><br /> | ||
| + | <math> \vec{j} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \rightarrow \varphi( \vec{j}) =\begin{pmatrix} 0 \\ -1 \end{pmatrix}</math><br /><br /> | ||
| + | <u>Matrix für die Spiegelung an der x-Achse</u>:<br /><br /> | ||
| + | <math> \begin{pmatrix} 1 \ 0 \\ 0 \ -1 \end{pmatrix} </math><br /><br /> | ||
| + | <u>Spiegelung eine Punktes P an der x-Achse:</u><br /> | ||
| + | <math> \vec{OP} = \begin{pmatrix} x \\ y \end{pmatrix}</math><br /><br /> | ||
| + | <math> \varphi( \vec{OP}) = \begin{pmatrix} 1 \ 0 \\ 0 \ -1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix}</math><br /><br /> | ||
| + | <u>'''Spiegelung an der x-Achse als lineare Abbildung:'''</u><br /> | ||
| + | Behauptung: <math> \varphi </math> ist eine lineare Abbildung.<br /><br /> | ||
| + | Zu zeigen:<br /> | ||
| + | (H) <math> \varphi </math> ist homogen<br /> | ||
| + | (A) <math> \varphi </math> ist additiv<br /><br /> | ||
| + | Beweis zur Homogenität:<br /> | ||
| + | Beweis zur Addidtivität:<br /><br /> | ||
| + | --[[Benutzer:Jessy*|Jessy*]] 09:15, 16. Jan. 2013 (CET)<br /><br /> | ||
| + | |||
| + | ==== Spiegelung an der y-Achse: ==== | ||
| + | <math> \vec{i} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \rightarrow \varphi( \vec{i}) = \begin{pmatrix} -1 \\ 0 \end{pmatrix}</math><br /><br /> | ||
| + | <math> \vec{j} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \rightarrow \varphi( \vec{j}) =\begin{pmatrix} 0 \\ 1 \end{pmatrix}</math><br /><br /> | ||
| + | <u>Matrix für die Spiegelung an der y-Achse</u>:<br /><br /> | ||
| + | <math> \begin{pmatrix} -1 \ 0 \\ 0 \ 1 \end{pmatrix} </math><br /><br /> | ||
| + | <u>Spiegelung eine Punktes P an der y-Achse:</u><br /> | ||
| + | <math> \vec{OP} = \begin{pmatrix} x \\ y \end{pmatrix}</math><br /><br /> | ||
| + | <math> \varphi( \vec{OP}) = \begin{pmatrix} -1 \ 0 \\ 0 \ 1 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix}</math><br /><br /> | ||
| + | <u>'''Spiegelung an der y-Achse als lineare Abbildung:'''</u><br /> | ||
| + | Behauptung: <math> \varphi </math> ist eine lineare Abbildung.<br /><br /> | ||
| + | Zu zeigen:<br /> | ||
| + | (H) <math> \varphi </math> ist homogen<br /> | ||
| + | (A) <math> \varphi </math> ist additiv<br /><br /> | ||
| + | Beweis zur Homogenität:<br /> | ||
| + | Beweis zur Addidtivität:<br /><br /> | ||
| + | --[[Benutzer:Jessy*|Jessy*]] 09:15, 16. Jan. 2013 (CET)<br /><br /> | ||
| + | |||
| + | ==== Spiegelung an der 1. Winkelhalbierenden: ==== | ||
| + | <math> \vec{i} = \begin{pmatrix} 1 \\ 0 \end{pmatrix} \rightarrow \varphi( \vec{i}) = \begin{pmatrix} 0 \\ 1 \end{pmatrix}</math><br /><br /> | ||
| + | <math> \vec{j} = \begin{pmatrix} 0 \\ 1 \end{pmatrix} \rightarrow \varphi( \vec{j}) =\begin{pmatrix} 1 \\ 0 \end{pmatrix}</math><br /><br /> | ||
| + | <u>Matrix für die Spiegelung an der 1. Winkelhalbbierenden</u>:<br /><br /> | ||
| + | <math> \begin{pmatrix} 0 \ 1 \\ 1 \ 0 \end{pmatrix} </math><br /><br /> | ||
| + | <u>Spiegelung eine Punktes P an der 1. Winkelhalbbierenden:</u><br /> | ||
| + | <math> \vec{OP} = \begin{pmatrix} x \\ y \end{pmatrix}</math><br /><br /> | ||
| + | <math> \varphi( \vec{OP}) = \begin{pmatrix} 0 \ 1 \\ 1 \ 0 \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix}</math><br /><br /> | ||
| + | <u>'''Spiegelung an der 1. Winkelhalbierenden als lineare Abbildung:'''</u><br /> | ||
| + | Behauptung: <math> \varphi </math> ist eine lineare Abbildung.<br /><br /> | ||
| + | Zu zeigen:<br /> | ||
| + | (H) <math> \varphi </math> ist homogen<br /> | ||
| + | (A) <math> \varphi </math> ist additiv<br /><br /> | ||
| + | Beweis zur Homogenität:<br /> | ||
| + | Beweis zur Addidtivität:<br /><br /> | ||
| + | --[[Benutzer:Jessy*|Jessy*]] 09:16, 16. Jan. 2013 (CET)<br /><br /> | ||
| + | |||
| + | ==Zentrische Streckung== | ||
| + | |||
| + | =Isomorphe Vektorräume= | ||
| + | {{Definition|Zwei Vektorräume sind isomorph zu einander, wenn sie durch eine bijektive lineare Abbildung aufeinander abgebildet werden können. }} | ||
<!--- hier drunter nichts eintragen ---> | <!--- hier drunter nichts eintragen ---> | ||
Aktuelle Version vom 16. Januar 2013, 10:21 Uhr
DefinitionDefinition (lineare Abbildung) Beispielesenkrechte Parallelprojektion auf die x-y-Ebene
Drehung
Drehungen um den Ursprung des Koordinatensystems
Drehung der kanonischen Basisvektoren Drehung um den Ursprung des Koordinatensystems als lineare Abbildung:Behauptung: GeradenspiegelungSpiegelung an der x-Achse:
Spiegelung an der y-Achse:
Spiegelung an der 1. Winkelhalbierenden:
Zentrische StreckungIsomorphe VektorräumeDefinition Zwei Vektorräume sind isomorph zu einander, wenn sie durch eine bijektive lineare Abbildung aufeinander abgebildet werden können. |
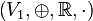 und
und  zwei Vektorräume über der Körper der reellen Zahlen.
zwei Vektorräume über der Körper der reellen Zahlen. 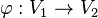 heißt lineare Abbildung wenn gilt:
heißt lineare Abbildung wenn gilt: 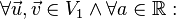
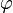 ist homogen:
ist homogen: 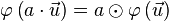
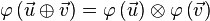
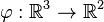
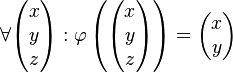
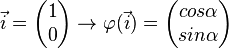
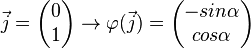
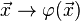
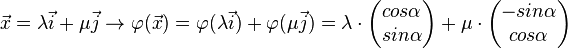
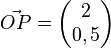 wird an O um
wird an O um 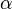 gedreht.
gedreht.