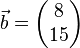Linearkombinationen 2012 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Jessy* (Diskussion | Beiträge) (→Lineare Abhängigkeit von zwei Vektoren) |
Jessy* (Diskussion | Beiträge) (→Lineare Abhängigkeit von zwei Vektoren) |
||
| (5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
{{Definition|(Linearkombination)<br />Als Linearkombination der Vektoren <math>\vec{v_1}, \vec{v_2}, ... , \vec{v_n}</math> bezeichnet man den Vektor<br /> <math>\vec{x}=\lambda_1\cdot \vec{v_1}+ \lambda_2 \cdot \vec{v_2} + ... + \lambda_n \cdot \vec{v_n}= \sum_{i=1}^n \lambda_i \cdot \vec{v_i}</math> (mit <math>\lambda_1, \lambda_2, ... ,\lambda_n \in \mathbb{R}</math>).}}<br /><br /> | {{Definition|(Linearkombination)<br />Als Linearkombination der Vektoren <math>\vec{v_1}, \vec{v_2}, ... , \vec{v_n}</math> bezeichnet man den Vektor<br /> <math>\vec{x}=\lambda_1\cdot \vec{v_1}+ \lambda_2 \cdot \vec{v_2} + ... + \lambda_n \cdot \vec{v_n}= \sum_{i=1}^n \lambda_i \cdot \vec{v_i}</math> (mit <math>\lambda_1, \lambda_2, ... ,\lambda_n \in \mathbb{R}</math>).}}<br /><br /> | ||
=Lineare Abhängigkeit= | =Lineare Abhängigkeit= | ||
| − | + | <u>Idee der linearen Abhängigkeit:</u> Es existiert ein Vektor der eine Linearkombination der anderen Vektoren ist.<br /><br /> | |
=== Lineare Abhängigkeit von zwei Vektoren === | === Lineare Abhängigkeit von zwei Vektoren === | ||
| − | Zwei Vektoren <math> \vec{a} </math> und <math> \vec{b} </math> sind linear abhängig, wenn sie ein Vielfaches voneinander sind.<br /><br /> | + | Zwei Vektoren <math> \vec{a} </math> und <math> \vec{b} </math> sind linear abhängig, wenn sie ein Vielfaches voneinander sind, bzw. wenn einer der beiden Vektoren ein Linearkombination des anderen ist.<br /> |
| + | Anders formuliert: Zwei Vektoren sind linear abhängig, wenn sie zur selben Pfeilklasse gehören, also parallel sind.<br /><br /> | ||
<u>Beispiel:</u><br /> | <u>Beispiel:</u><br /> | ||
<math> \vec{a} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} </math> und <math> \vec{b} = \begin{pmatrix} 8 \\ 12 \end{pmatrix} </math><br /><br /> | <math> \vec{a} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} </math> und <math> \vec{b} = \begin{pmatrix} 8 \\ 12 \end{pmatrix} </math><br /><br /> | ||
<math> 4 \cdot \vec{a} = \vec{b} </math><br /><br /> | <math> 4 \cdot \vec{a} = \vec{b} </math><br /><br /> | ||
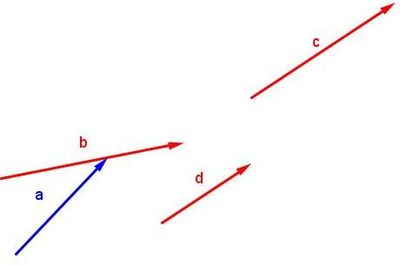
| − | [[Bild: | + | [[Bild:LA_zu_einem_Vektor2.JPG|500px]] Die Vektoren <math> \vec{b}, \vec{c}, \vec{d} </math> sind linearabhängig zu <math> \vec{a} </math><br /><br /> |
<u>Gegenbeispiel:</u><br /> | <u>Gegenbeispiel:</u><br /> | ||
<math> \vec{a} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} </math> und <math> \vec{b} = \begin{pmatrix} 8 \\ 15 \end{pmatrix} </math><br /><br /> | <math> \vec{a} = \begin{pmatrix} 2 \\ 3 \end{pmatrix} </math> und <math> \vec{b} = \begin{pmatrix} 8 \\ 15 \end{pmatrix} </math><br /><br /> | ||
Es gibt keine reelle Zahl, die mit <math> \vec{a} </math> multipliziert den <math> \vec{b} </math> ergibt.<br /><br /> | Es gibt keine reelle Zahl, die mit <math> \vec{a} </math> multipliziert den <math> \vec{b} </math> ergibt.<br /><br /> | ||
| + | [[Bild:LUA_zu_einem_Vektor.JPG|400px]] Die Vektoren <math> \vec{b}, \vec{c}, \vec{d} </math> sind nicht linearabhängig zu <math> \vec{a} </math><br /><br /> | ||
--[[Benutzer:Jessy*|Jessy*]] 18:36, 18. Jan. 2013 (CET) | --[[Benutzer:Jessy*|Jessy*]] 18:36, 18. Jan. 2013 (CET) | ||
Aktuelle Version vom 18. Januar 2013, 20:09 Uhr
Darstellung von Vektoren mittels anderer Vektoren
LinearkombinationenDefinition (Linearkombination) Lineare AbhängigkeitIdee der linearen Abhängigkeit: Es existiert ein Vektor der eine Linearkombination der anderen Vektoren ist. Lineare Abhängigkeit von zwei VektorenZwei Vektoren |
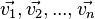 bezeichnet man den Vektor
bezeichnet man den Vektor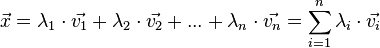 (mit
(mit 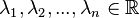 ).
).
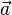 und
und 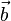 sind linear abhängig, wenn sie ein Vielfaches voneinander sind, bzw. wenn einer der beiden Vektoren ein Linearkombination des anderen ist.
sind linear abhängig, wenn sie ein Vielfaches voneinander sind, bzw. wenn einer der beiden Vektoren ein Linearkombination des anderen ist.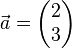 und
und 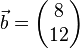
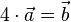
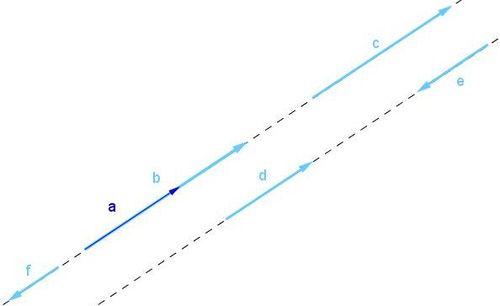
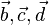 sind linearabhängig zu
sind linearabhängig zu