Quiz der Woche
Aus Geometrie-Wiki
Version vom 16. Mai 2010, 16:31 Uhr von *m.g.* (Diskussion | Beiträge)
Es sei 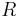 ein Äquivalenzrelation auf der Menge
ein Äquivalenzrelation auf der Menge  . Wir zerlegen
. Wir zerlegen  derart in Teilmengen
derart in Teilmengen 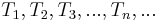 , dass gilt: Jede der Teilmengen besteht aus all den Elementen von
, dass gilt: Jede der Teilmengen besteht aus all den Elementen von  , die in der Relation
, die in der Relation 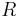 zueinander stehen.
zueinander stehen.
Übung zur Generierung einer Klasseneinteilung entsprechend obiger Idee.
Wir gehen von der folgenden Menge  aus:
aus: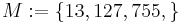
| Insekt | Käfer |  |
Ameise | Motte | |
| Obst | Pflaume |  |
Apfel | Kirsche | Banane |
| Nutztier | Datei:Gluecks schwein.jpg | Schaf | Rind |
Im folgenden soll bewiesen werden, dass die so gewonnenen Teilmengen von  eine Klasseneinteilung von
eine Klasseneinteilung von  sind. Ergänzen Sie dementsprechend die folgenden Ausführungen:
sind. Ergänzen Sie dementsprechend die folgenden Ausführungen:

