Serie 02 zum 01.11.19: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 02.05) |
||
| Zeile 18: | Zeile 18: | ||
= Aufgabe 02.05 = | = Aufgabe 02.05 = | ||
| − | Es sei <math>\overline{ABC}</math> ein rechtwinkliges | + | Es sei <math>\overline{ABC}</math> ein rechtwinkliges Dreieck mit einem Innenwinkel der Größe <math>30^\circ</math>. |
Beweisen Sie:<br /> | Beweisen Sie:<br /> | ||
Wenn die Hypotenuse des Dreiecks die Länge 1 hat, dann haben die Katheten dieses Dreiecks die Längen <math>\frac{1}{2}</math> und <math>\frac{1}{2} \sqrt{3}</math>. | Wenn die Hypotenuse des Dreiecks die Länge 1 hat, dann haben die Katheten dieses Dreiecks die Längen <math>\frac{1}{2}</math> und <math>\frac{1}{2} \sqrt{3}</math>. | ||
Version vom 20. Oktober 2019, 14:32 Uhr
|
Aufgabe 02.01Es seien Aufgabe 02.02Beweisen Sie: Wenn das Quadrat einer natürlichen Zahl Aufgabe 02.03Sie dürfen den Nebenwinkelsatz voraussetzen. Beweisen Sie den Scheitelwinkelsatz. Aufgabe 02.04Sie dürfen den Nebenwinkelsatz und den Innenwinkelsatz für Dreiecke voraussetzen. Beweisen Sie: Jeder Außenwinkel eines Dreiecks ist so groß wie die Summe der Größen der beiden nichtanliegenden Innenwinkel dieses Dreiecks. Aufgabe 02.05Es sei Aufgabe 02.06Aufgabe 02.07Aufgabe 01.08Aufgabe 02.09Aufgabe 02.10 |
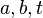 drei natürliche Zahlen.
drei natürliche Zahlen.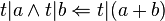
 gerade ist, dann ist
gerade ist, dann ist  ein rechtwinkliges Dreieck mit einem Innenwinkel der Größe
ein rechtwinkliges Dreieck mit einem Innenwinkel der Größe 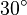 .
Beweisen Sie:
.
Beweisen Sie: und
und 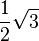 .
.

