Serie 1: Geraden in der Ebene, zwei Gleichungen mit zwei Unbekannten SoSe 2018: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 1.1 SoSe 2018) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 1.7 SoSe 2018) |
||
| (9 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 10: | Zeile 10: | ||
=Aufgabe 1.2 SoSe 2018= | =Aufgabe 1.2 SoSe 2018= | ||
Überführen Sie eine Gleichung vom Typ <math>y=mx+n ~(m, n \in \mathbb{R}, x,y \in \mathbb{R})</math> in eine Gleichung vom Typ <math>ax+by=c~(a,b,c \in \mathbb{R}, a^2+b^2 \not = 0, x,y \in \mathbb{R})</math>. | Überführen Sie eine Gleichung vom Typ <math>y=mx+n ~(m, n \in \mathbb{R}, x,y \in \mathbb{R})</math> in eine Gleichung vom Typ <math>ax+by=c~(a,b,c \in \mathbb{R}, a^2+b^2 \not = 0, x,y \in \mathbb{R})</math>. | ||
| + | |||
| + | =Aufgabe 1.3 SoSe 2018= | ||
| + | Gegeben seien in der reellen Zahlenebene die beiden Punkte <math>A\left (\frac{1}{2}|\frac{3}{4} \right )</math> und <math>B \left ( \frac{3}{4} |- \frac{1}{2} \right )</math>. Geben Sie eine Gleichung zur Beschreibeung von <math>AB</math> an. | ||
| + | |||
| + | =Aufgabe 1.4 SoSe 2018= | ||
| + | Gegeben seien die beiden Punkte <math>A(4 \vert 3)</math> und <math>B(-2 \vert -2)</math>.<br /> | ||
| + | a) Geben Sie einen Richtungsvektor <math>\overrightarrow{r}</math> für die Gerade <math>AB</math> an.<br /> | ||
| + | b) Geben Sie einen Vektor <math>\overrightarrow{n}</math> an, der senkrecht auf <math>AB</math> steht.<br /> | ||
| + | c) Erläutern Sie den Zusammenhang zwischen <math>\overrightarrow{r}</math> und <math>\overrightarrow{n}</math>. <br /> | ||
| + | d) Geben Sie eine Gleichung vom Typ <math>ax+by=c</math> für <math>AB</math> an.<br /> | ||
| + | e) Geben Sie eine Gleichung vom Typ <math>y=mx+n</math> für <math>AB</math> an.<br /> | ||
| + | |||
| + | =Aufgabe 1.5 SoSe 2018= | ||
| + | Eine Gerade <math>g</math> möge die <math>x-</math>Achse im Punkt <math>A(\sqrt{2} \vert 0)</math> unter einem Winkel von <math>30^\circ</math> schneiden. Geben Sie 3 verschiedene Gleichungen zur Beschreibung von <math>g</math> an. | ||
| + | |||
| + | =Aufgabe 1.6 SoSe 2018= | ||
| + | Es sei <math>\overline{ABCD}</math> eine Raute. Der Schnittpunkt der Diagonalen dieser Raute möge der Koordinatenursprung sein. Der Punkt <math>A</math> liege auf der negativen <math>x-</math>Achse, der Punkt <math>B</math> auf der negativen <math>y-</math>Achse. Beschreiben Sie die Geraden <math>AB, BC, CD, DA</math> mittels Gleichungen in Abhängigkeit von den Diagonalenlängen <math>\vert AC \vert</math> und <math>\vert BC \vert</math>. | ||
| + | |||
| + | =Aufgabe 1.7 SoSe 2018= | ||
| + | Auf einem Mobiltelefon befindet sich ein Prepaid-Guthaben von 20 €. Eine SMS | ||
| + | kostet 0,15 €, eine Minute Telefonieren 0,20 €. Wie viele Minuten lang kann | ||
| + | mit dem Guthaben telefoniert und wie viele SMS können verschickt werden?<br /> | ||
| + | |||
| + | (Filler, Beispiel 1.1, Seite 2) | ||
| + | |||
| + | =Aufgabe 1.8 SoSe 2018= | ||
| + | Lösen Sie die folgende Aufgabe grafisch:<br /> | ||
| + | Aus einem alten Rechenbuch: Eine Anzahl von Personen hatte in einem | ||
| + | Gasthaus eine Zeche zu bezahlen. Zahlte jede 4,35 Mark, so fehlten noch | ||
| + | 20 Pf an der ganzen Summe. Zahlte jede 4,40 Mark, so waren es 20 Pf | ||
| + | zuviel. Wie groß war die zu zahlende Summe? Wie viele Personen waren es?<br /> | ||
| + | (Filler, Aufgabe 10, Seite 14) | ||
<!--- hier drunter nichts eintragen ---> | <!--- hier drunter nichts eintragen ---> | ||
Aktuelle Version vom 28. April 2018, 13:42 Uhr
Aufgabe 1.1 SoSe 2018Überführen Sie eine Gleichung vom Typ Aufgabe 1.2 SoSe 2018Überführen Sie eine Gleichung vom Typ Aufgabe 1.3 SoSe 2018Gegeben seien in der reellen Zahlenebene die beiden Punkte Aufgabe 1.4 SoSe 2018Gegeben seien die beiden Punkte Aufgabe 1.5 SoSe 2018Eine Gerade Aufgabe 1.6 SoSe 2018Es sei Aufgabe 1.7 SoSe 2018Auf einem Mobiltelefon befindet sich ein Prepaid-Guthaben von 20 €. Eine SMS
kostet 0,15 €, eine Minute Telefonieren 0,20 €. Wie viele Minuten lang kann
mit dem Guthaben telefoniert und wie viele SMS können verschickt werden? (Filler, Beispiel 1.1, Seite 2) Aufgabe 1.8 SoSe 2018Lösen Sie die folgende Aufgabe grafisch: |
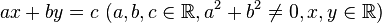 in eine Gleichung vom Typ
in eine Gleichung vom Typ 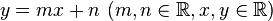 .
.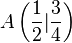 und
und 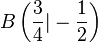 . Geben Sie eine Gleichung zur Beschreibeung von
. Geben Sie eine Gleichung zur Beschreibeung von  an.
an.
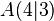 und
und 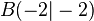 .
.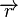 für die Gerade
für die Gerade 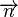 an, der senkrecht auf
an, der senkrecht auf  für
für 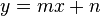 für
für  möge die
möge die 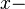 Achse im Punkt
Achse im Punkt 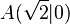 unter einem Winkel von
unter einem Winkel von 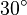 schneiden. Geben Sie 3 verschiedene Gleichungen zur Beschreibung von
schneiden. Geben Sie 3 verschiedene Gleichungen zur Beschreibung von  eine Raute. Der Schnittpunkt der Diagonalen dieser Raute möge der Koordinatenursprung sein. Der Punkt
eine Raute. Der Schnittpunkt der Diagonalen dieser Raute möge der Koordinatenursprung sein. Der Punkt  liege auf der negativen
liege auf der negativen  auf der negativen
auf der negativen 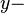 Achse. Beschreiben Sie die Geraden
Achse. Beschreiben Sie die Geraden 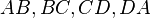 mittels Gleichungen in Abhängigkeit von den Diagonalenlängen
mittels Gleichungen in Abhängigkeit von den Diagonalenlängen 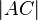 und
und 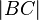 .
.

