Strecken, Pfeile und Pfeilklassen SoSe 2017: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Die Gruppe der Pfeilklassen) |
*m.g.* (Diskussion | Beiträge) (→Die Gruppe der Pfeilklassen) |
||
| Zeile 46: | Zeile 46: | ||
# Inverse Elemente: <math>\forall \overrightarrow{a} \in \overrightarrow{\mathbb{P}} \exists -\overrightarrow{a}: \overrightarrow{a} \oplus -\overrightarrow{a} = \overrightarrow{o} </math> | # Inverse Elemente: <math>\forall \overrightarrow{a} \in \overrightarrow{\mathbb{P}} \exists -\overrightarrow{a}: \overrightarrow{a} \oplus -\overrightarrow{a} = \overrightarrow{o} </math> | ||
# Kommutativität: <math>\forall \overrightarrow{a}, \overrightarrow{b} \in \overrightarrow{\mathbb{P}}: \overrightarrow{a} \oplus \overrightarrow{b} = \overrightarrow{b} \oplus \overrightarrow{a}</math>. | # Kommutativität: <math>\forall \overrightarrow{a}, \overrightarrow{b} \in \overrightarrow{\mathbb{P}}: \overrightarrow{a} \oplus \overrightarrow{b} = \overrightarrow{b} \oplus \overrightarrow{a}</math>. | ||
| + | Beweis: Übungsaufgabe | ||
<!--- hier drunter nichts eintragen ---> | <!--- hier drunter nichts eintragen ---> | ||
Version vom 4. Juni 2017, 13:48 Uhr
StreckenDefinitionDefinition: (Strecke
BemerkungIm Gegensatz zur Definition des Begriffs Strecke in der Einführung in die Geometrie lassen wir hier zu, dass die Punkte gerichtete Strecken bzw PfeileDefinition: (gerichtete Strecke
PfeilklassenDefinition: (Pfeilgleichheit)
Satz: (Pfeilgleichheit ist ÄR)
Beweis: Übungsaufgabe Definition: (Pfeilklasse)
Hinweis: Jede Pfeilklasse ist durch Angabe eines ihrer Repräsentanten eindeutig bestimmt. Ob wir mit Addition von PfeilklassenDefinition: (Addition von Pfeilklassen)
Satz: (Wohldefiniertheit der Operation
Beweis : ÜA Die Pfeilklasse
|
 )
)
 und
und  zwei beliebige Punkte. Unter der Strecke
zwei beliebige Punkte. Unter der Strecke 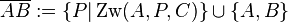 .
.
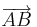 )
)
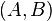 und nennen
und nennen 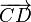 stehen in der Relation pfeilgleich zueinander, wenn
stehen in der Relation pfeilgleich zueinander, wenn 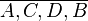 ein Parallelogramm ist. In Zeichen:
ein Parallelogramm ist. In Zeichen: 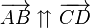
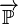
 meint einen bestimmten Pfeil und
meint einen bestimmten Pfeil und 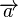 bezeichnet die Pfeilklasse, die durch
bezeichnet die Pfeilklasse, die durch 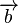 zwei Pfeilklassen. Die Addition
zwei Pfeilklassen. Die Addition 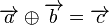 ist wie folgt definiert: Es seien
ist wie folgt definiert: Es seien 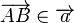 und
und 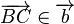 .
.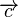 ist die Pfeilklasse, die durch den Pfeil
ist die Pfeilklasse, die durch den Pfeil 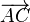 eindeutig bestimmt ist.
eindeutig bestimmt ist.
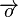
![\left[\overrightarrow{\mathbb{P}}, \oplus\right]](/images/math/0/f/b/0fb620f4c323ea8d8774437de1297584.png) ist eine abelsche Gruppe:
ist eine abelsche Gruppe: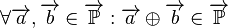
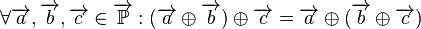
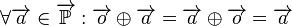
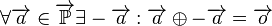
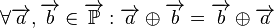 .
.

