Tangentenkriterium: Unterschied zwischen den Versionen

Version vom 24. Juli 2011, 10:53 Uhr

Inhaltsverzeichnis

1 Tangentenkriterium

Tangentenkriterium

Kriterium: (Tangete am Kreis)

Eine Gerade t, die durch einen Punkt A eines Kreises k mit dem Mittelpunkt M verläuft, ist genau dann Tangente an k, wenn t senkrecht auf MA steht.

Satz 1: (Tangete am Kreis)

$\ t \cap k = \lbrace A\rbrace \Rightarrow MA \perp \ t$

Beweis durch Wiederspruch:
Voraussetzung: $\ t \cap k = \lbrace A\rbrace$
Behauptung: 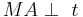$MA \perp \ t$

Annahme: 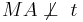$\ MA \not\perp \ t$

1	Es existiert ein Lot von M auf t, dieses ist eindeutig. Der Lotfußpunkt auf k heiße B.	Ex. und Eindeutigkeit Lot, Annahme, Voraussetzung
2	CB\| = \|BA\|	Axiom vom Lineal, Abstandsaxiom, Definition zwischenrelation, Voraussetzung, (1) und Skizze
3	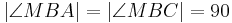$\|\angle MBA \| = \|\angle MBC\| = 90$	nach Konstruktion, Def. NW, Def. supplementär, Supplementaxiom, Def. Lot (1)
4	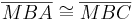$\overline{MBA} \cong \overline{MBC}$	MB\| = \|MB\|
5	MC\| = \|MA\| = r nach Voraussetzung und es ergeben sich zwei Schnittpunkte, was ein Widerspruch zur Voraussetzung ist.

Satz 2: (Tangente am Kreis)

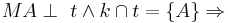$MA \perp \ t \wedge k \cap t = \lbrace A\rbrace \Rightarrow$ t ist Tangente an k.

Eigentlich erscheint dieser Beweis komisch. Allerdings könnte es ja sein, dass wenn eine Gerade durch eben einen Punkt A verläuft und senkrecht auf dem Berührradius steht, dass dann trotzdem ein zweiter Schnittpunkt vorhanden ist mit k und dann wäre halt t keine Tangente mehr.

Voraussetzung: 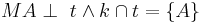$MA \perp \ t \wedge k \cap t = \lbrace A\rbrace$
Behauptung: t ist Tangente an k
Annahme: Es ex. ein Punkt S: 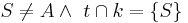$S \neq A \wedge \ t \cap k = \lbrace S\rbrace$

Ich versuche diesen Beweis bewusst in der absoluten Geometrie zu Beweisen. Mit der Innenwinklesumme wäre es natürlich noch einfacher, aber zwecks der Übung.

1	$\left\| MA \right\| = \left\| MS \right\|$	Annahme, Definiton Kreis und Radius
2	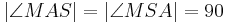$\|\angle MAS\| = \|\angle MSA\| = 90$	Voraussetzung, Basiswinkelsatz, (1), Def. Senkrecht
3	Demnach sind im Dreieck zwei Winkel nicht spitz, was ein Widerspruch zu einem der Korollare ist. Demnach ist die Annahme zu verwerfen.	Korollar des schwachen Außenwinkelsatzes, (2), Definition Dreieck

--Flo60 10:53, 24. Jul. 2011 (CEST)

@@ Zeile 29: / Zeile 29: @@
 ===== Satz 2: (Tangente am Kreis) =====
-::<math>MA \perp \ t \wedge k \cap t = \lbrace A\rbrace  \Rightarrow     </math> <br /> t ist Tangente an k.
+::<math>MA \perp \ t \wedge k \cap t = \lbrace A\rbrace  \Rightarrow     </math> t ist Tangente an k. <br />
+<br />
+<br />
+Eigentlich erscheint dieser Beweis komisch. Allerdings könnte es ja sein, dass wenn eine Gerade durch eben einen Punkt A verläuft und senkrecht auf dem Berührradius steht, dass dann trotzdem ein zweiter Schnittpunkt vorhanden ist mit k und dann wäre halt t keine Tangente mehr.
+<br />
+<br />
+Voraussetzung: <math>MA \perp \ t \wedge k \cap t = \lbrace A\rbrace </math><br />
+Behauptung: t ist Tangente an k <br />
+Annahme: Es ex. ein Punkt S: <math>S \neq A \wedge \ t \cap k = \lbrace   S\rbrace</math>
+<br />
+<br />
+Ich versuche diesen Beweis bewusst in der absoluten Geometrie zu Beweisen. Mit der Innenwinklesumme wäre es natürlich noch einfacher, aber zwecks der Übung.
+<br />
+<br />
+{| class="wikitable"
+|-
+| 1 || <math>\left| MA \right| = \left| MS \right| </math> || Annahme, Definiton Kreis und Radius
+|-
+| 2 || <math>|\angle MAS| = |\angle MSA| = 90 </math> || Voraussetzung, Basiswinkelsatz, (1), Def. Senkrecht
+|-
+| 3 || Demnach sind im Dreieck zwei Winkel nicht spitz, was ein Widerspruch zu einem der Korollare ist. Demnach ist die Annahme zu verwerfen. || Korollar des schwachen Außenwinkelsatzes, (2), Definition Dreieck
+|}
+<br />--[[Benutzer:HecklF|Flo60]] 10:53, 24. Jul. 2011 (CEST)

Tangentenkriterium: Unterschied zwischen den Versionen

Version vom 24. Juli 2011, 10:53 Uhr

Inhaltsverzeichnis