Was ist eine Gruppe? SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Beispiele für Gruppen) |
*m.g.* (Diskussion | Beiträge) (→Gruppendefinitionen) |
||
| Zeile 10: | Zeile 10: | ||
=Gruppendefinitionen= | =Gruppendefinitionen= | ||
| + | ==Die "übliche" Gruppendefinition (lange Version)== | ||
| + | {{Definition|1= Es sei <math>G</math> eine nichtleere Menge auf der eine Verknüpfung <math>\odot</math>. <br /> | ||
| + | Wenn die folgenden Axiome erfüllt sind, heißt die Struktur <math>\mathbb{G}:=[G, \odot ]</math> Gruppe:<br /> | ||
| + | # <math>\odot</math> ist auf <math>G</math> abgeschlossen: <math>\forall a,b \in G: a \odot b \in G</math> | ||
| + | # <math>\odot</math> ist assoziativ auf <math>G</math>: <math>\forall a, b, c \in G: (a \odot b) \odot c = a \odot (b \odot c)</math> | ||
| + | # Bezüglich <math>\odot</math> existiert in <math>G</math> ein ("universelles") Einslement <math>e</math>: <math>\exist e \in G \forall a \in G: a \odot e = e \odot a= a </math>. | ||
| + | # Bezüglich <math>\odot</math> existiert zu jedem <math>a</math> aus <math>G</math> ein ("persönliches") inverses Element <math>a^{-1}</math>: <math>\forall a \in G \exist a^{-1} \in G: a \odot a^{-1} = a^{-1} \odot a = e</math>. | ||
| + | }} | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Algebra]] | [[Kategorie:Algebra]] | ||
Version vom 1. Mai 2017, 13:05 Uhr
Beispiele für Gruppenendliche GruppenDie Gruppe der Deckabbildungen des RechtecksDie Gruppe der Deckabbildungen der RauteGegenbeispiele für GruppenGruppendefinitionenDie "übliche" Gruppendefinition (lange Version)Definition Es sei
|
eine nichtleere Menge auf der eine Verknüpfung 
. ![\mathbb{G}:=[G, \odot ]](/images/math/b/6/2/b62276da8758fad83c54ead688c9ecca.png)
Gruppe:
: 
.
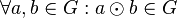
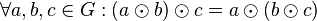
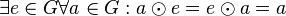aus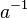 
: 
.
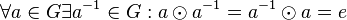