Übung Aufgaben 13 (WS 14/15)
Aus Geometrie-Wiki
Inhaltsverzeichnis |
Aufgabe 13.1
Das Dreieck  wird an Punkt D um 90 gedreht. Das gedrehte Dreieck wird nun um den eingezeichneten Vektor verschoben. Gibt es einen Punkt der Ebene, der nun genau wieder an seinem ursprünglichen Ort liegt? Konstruieren Sie ggf. diesen Punkt und begründen Sie!
wird an Punkt D um 90 gedreht. Das gedrehte Dreieck wird nun um den eingezeichneten Vektor verschoben. Gibt es einen Punkt der Ebene, der nun genau wieder an seinem ursprünglichen Ort liegt? Konstruieren Sie ggf. diesen Punkt und begründen Sie!
Lösung von Aufgabe 13.1P (WS_14/15)
Aufgabe 13.2
Zeigen Sie, dass die Verkettung einer Drehung 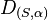 mit einer Verschiebung wieder eine Drehung
mit einer Verschiebung wieder eine Drehung 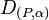 ergibt. Wo liegt das neue Drehzentrum P?
ergibt. Wo liegt das neue Drehzentrum P?
Lösung von Aufgabe 13.2P (WS_14/15)
Aufgabe 13.3
Zeigen Sie, dass bei der Verkettung einer Schubspiegelung 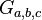 (
(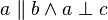 ) mit einer Spiegelung
) mit einer Spiegelung 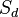 (
(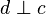 ) eine Punktspiegelung entsteht.
) eine Punktspiegelung entsteht.
Lösung von Aufgabe 13.3P (WS_14/15)
Aufgabe 13.4
Beweisen Sie den Innenwinkelsatz für Dreiecke mit Hilfe zweier Punktspiegelungen.
Lösung von Aufgabe 13.4P (WS_14/15)

