Übung Aufgaben 6 (SoSe 15)
Inhaltsverzeichnis |
Aufgabe 6.1
Unter einem Dreieck versteht man die Vereinigungsmenge von drei besonderen Strecken (umgangssprachlich: Das Dreieck ist sein Rand.). Definieren Sie den Begriff Dreieck  .
.
Lösung von Aufg. 6.1P (SoSe_15)
Aufgabe 6.2
Definieren Sie mittels des Schnitts geeigneter Halbebenen den Begriff des Inneren eines Dreiecks  .
.
Lösung von Aufg. 6.2P (SoSe_15)
Aufgabe 6.3
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
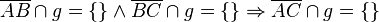
(Hinweis: Nehmen Sie einen weiteren Punkt D an, mit 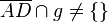 und nutzen Sie den Satz von Pasch)
und nutzen Sie den Satz von Pasch)
Lösung von Aufg. 6.3P (SoSe_15)
Aufgabe 6.4
Wir gehen von folgender Definition aus: Ein rechter Winkel ist ein Winkel, der das gleiche Maß wie einer seiner Nebenwinkel hat. Außerdem gelte Satz IV.2: Nebenwinkel sind supplementär.
Beweisen Sie: Jeder rechte Winkel hat das Maß 90.

