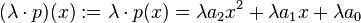Übungen 05
Inhaltsverzeichnis[Verbergen] |
Pfeilklassen und  Vektorräume
Vektorräume
Aufgabe 5.1
Ein Vektor 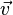 wird durch einen Pfeil
wird durch einen Pfeil 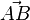 repräsentiert. Geben Sie
repräsentiert. Geben Sie  als Zahlentripel an.
als Zahlentripel an.
a) A(-8,5,12), B(-5,7,-11)
b) A(5,6,7), B(-3,9,-4)
Aufgabe 5.2
Gegeben ist eine Verschiebung 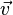 des Raumes durch einen Verschiebungspfeil
des Raumes durch einen Verschiebungspfeil 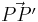 mit
mit 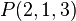 und
und 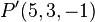 .
.
a) Geben Sie den Verschiebungsvektor 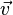 als Zahlentripel an.
als Zahlentripel an.
b) Geben Sie die Koordinaten der Bildpunkte der Punkte 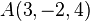 und
und 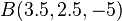 bei der Verschiebung
bei der Verschiebung  an.
an.
Aufgabe 5.3
Durch 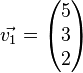 und
und 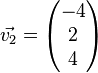 werden zwei Verschiebungen des Raumes beschrieben.
werden zwei Verschiebungen des Raumes beschrieben.
a) Der Punkt 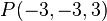 wird zunächst um
wird zunächst um 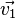 und dann um
und dann um 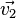 verschoben. Geben Sie die Koordinaten der entsprechenden Bildpunkt
verschoben. Geben Sie die Koordinaten der entsprechenden Bildpunkt 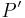 und
und 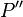 an.
an.
b) Geben Sie den Verschiebungsvektor 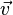 an, der die Nacheinanderausfürhugn der Verschiebungen
an, der die Nacheinanderausfürhugn der Verschiebungen 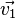 und
und 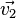 beschreibt.
beschreibt.
Aufgabe 5.4
Zeigen Sie, dass die Menge 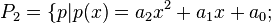 mit
mit 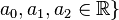 der Polynome höchstens 2. Grades mit der folgend definierten Verknüpfungen
der Polynome höchstens 2. Grades mit der folgend definierten Verknüpfungen 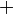 und
und  für beliebige
für beliebige 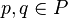 mit
mit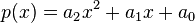 und
und 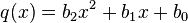 sowie
sowie 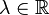 ein Vektorraum ist:
ein Vektorraum ist:
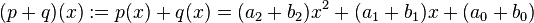 ,
,