Übungsaufgaben Elementargeometrie SoSe 2020, Eigenschaften von Bewegungen und Fixpunkte, Fixgerade
Inhaltsverzeichnis[Verbergen] |
Übungsaufgaben zum Thema
Aufgabe 1.1
Satz 1.7: Eindeutige Bestimmtheit von Bewegungen durch ein Dreieck und dessen Bild
Jede Bewegung  ist durch drei nichtkollineare Punkte
ist durch drei nichtkollineare Punkte  und deren Bilder
und deren Bilder 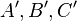 eindeutig bestimmt.
eindeutig bestimmt.
Der Satz ist wie folgt zu verstehen: Anstelle einer allgemeinen Abbildungsvorschrift für eine Bewegung  kann man auch eine Dreieck
kann man auch eine Dreieck  und dessen Bild
und dessen Bild 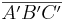 bei
bei  vorgeben und für jeden weiteren Punkt
vorgeben und für jeden weiteren Punkt  ist sein Bild
ist sein Bild 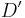 bei
bei  eindeutig bestimmt.
eindeutig bestimmt.
Beweisen Sie Satz 1.7
Hinweis: Geben Sie sich ein Dreieck und dessen Bild vor und konstruieren Sie dann für einen beliebigen Punkt  sein Bild. Beschreiben Sie dann ihre Konstruktion und Sie haben den Beweis.
sein Bild. Beschreiben Sie dann ihre Konstruktion und Sie haben den Beweis.
Aufgabe 1.2
Es seien 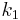 und
und 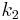 zwei Kreise mit den Mittelpunkten
zwei Kreise mit den Mittelpunkten 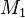 und
und  . Der Schnitt
. Der Schnitt 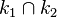 möge aus genau den beiden Punkten
möge aus genau den beiden Punkten 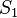 und
und 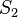 bestehen. Ein dritter Kreis
bestehen. Ein dritter Kreis 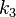 mit dem Mittelpunkt
mit dem Mittelpunkt 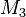 möge ebefalls durch die beiden Punkte
möge ebefalls durch die beiden Punkte 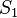 und
und 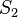 gehen. Beweisen Sie
gehen. Beweisen Sie 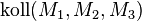 .
.
Aufgabe 2.1 Fixgeraden einer Spiegelung
Es sei 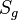 die Spiegelung an der Geraden
die Spiegelung an der Geraden  . Es gibt unendlich viele Geraden, die bzgl.
. Es gibt unendlich viele Geraden, die bzgl. 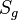 Fixgeraden aber keine Fixpunktgeraden sind. Beschreiben Sie diese Geraden.
Fixgeraden aber keine Fixpunktgeraden sind. Beschreiben Sie diese Geraden.
Aufgabe 2.2 Fixpunkte bei der Zentralprojektion
Wir betrachten alle Punkte des Raumes. Die sogenannte Zentralprojektion 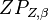 bildet diese Punkte auf eine Bildebene
bildet diese Punkte auf eine Bildebene  ab. Hierzu bestimmt man einen sogenannten Zentralpunkt außerhalb von
ab. Hierzu bestimmt man einen sogenannten Zentralpunkt außerhalb von  . Es sei
. Es sei 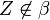 dieser Zentralpunkt. Das Bild eines beliebigen Punktes
dieser Zentralpunkt. Das Bild eines beliebigen Punktes  ist der Schnittpunkt der Geraden
ist der Schnittpunkt der Geraden 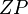 mit der Bildebene
mit der Bildebene  :
: 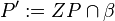 .
.
- Bezüglich eines Punktes ist
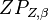 keine Abbildung. Welcher Punkt des Raumes ist das? Begründen Sie Ihre Antwort.
keine Abbildung. Welcher Punkt des Raumes ist das? Begründen Sie Ihre Antwort.
-
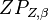 hat unendlich viele Fixpunkte . Beschreiben Sie diese.
hat unendlich viele Fixpunkte . Beschreiben Sie diese.
-
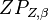 hat unendlich viele Fixpunktgeraden, jedoch keine Fixgerade, die nicht gleichzeitig Fixpunktgerade ist. Erklären Sie diesen Sachverhalt.
hat unendlich viele Fixpunktgeraden, jedoch keine Fixgerade, die nicht gleichzeitig Fixpunktgerade ist. Erklären Sie diesen Sachverhalt.
- Ist
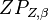 geradentreu? Begründen Sie Ihre Antwort.
geradentreu? Begründen Sie Ihre Antwort.
- Für einige Winkel ist
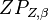 winkeltreu. Für welche?
winkeltreu. Für welche?
- Der Zentralpunkt einer zentrischen Streckung ist Fixpunkt dieser zentrischen Streckung. Warum ist der Zentralpunkt einer Zentralprojektion kein Fixpunkt dieser Zentralprojektion?
Aufgabe 2.3 Klassifikation von Bewegungen nach fixen Elementen
Im Laufe des Semesters werden wir beweisen, dass es genau vier Typen von Bewegungen gibt:
- Geradenspiegelungen
- Drehungen
- Verschiebungen
- Schubspiegelungen (NAF von Verschiebung und Geradenspiegelung)
Die Identität gilt als Spezialfall sowohl der Verschiebungen als auch der Drehungen. Die Identität lassen Sie bitte bei den Folgenden Betrachtungen außen vor.\\ Ordnen Sie diese Typen von Bewegungen den folgenden Eigenschaften zu:
- Die Bewegung hat keinen Fixpunkt.
- Die Bewegung hat genau einen Fixpunkt.
- Die Bewegung hat genau zwei Fixpunkte.
- Die Bewegung hat genau eine Fixpunktgerade.
- Die Bewegung hat mehr als drei paarweise verschiedene Fixpunkte.
- Die Bewegung hat genau drei nichtkollineare Fixpunkte.
- Die Bewegung hat genau eine Fixgerade.
- Die Bewegung hat keine Fixpunktgerade.
Aufgabe 2.4 Berechnung eines Fixpunktes
Wir betrachten die NAF der beiden Geradenspiegelungen 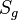 und
und 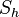 . Die Spiegelachsen
. Die Spiegelachsen  und
und  werden bzgl. eines kartesischen Koordinatensytems wie folgt beschrieben:
werden bzgl. eines kartesischen Koordinatensytems wie folgt beschrieben:
- g:
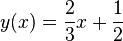
- h:
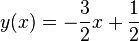
Geben Sie die Koordinaten des Fixpunktes von 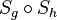 an.
an.

