13.06.2012: Konvexe Punktmengen

Platz für Anregungen und Diskussionen zur heutigen Übungsveranstaltung (13.06.2012)

Ergänzend zur heutigen Veranstaltung noch ein Vorschlag des Mittelpunktbeweises eines Kommilitonen. Hierbei wird von Anfang an davon ausgegangen, dass 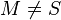$M\ne S$ und somit 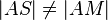$|AS|\ne |AM|$ gilt. Beweis passt und ist eine andere Möglichkeit, den Beweis zu beginnen. Schlussendlich ist er vom Prinzip her gleich zu dem, den wir in der Veranstaltung gemacht haben - auch hier führen wir auf die Gesamtstreckenlänge von $\overline{AB}$ (oder wie hier $\overline{AC}$ zurück. Trotzdem gute Idee!


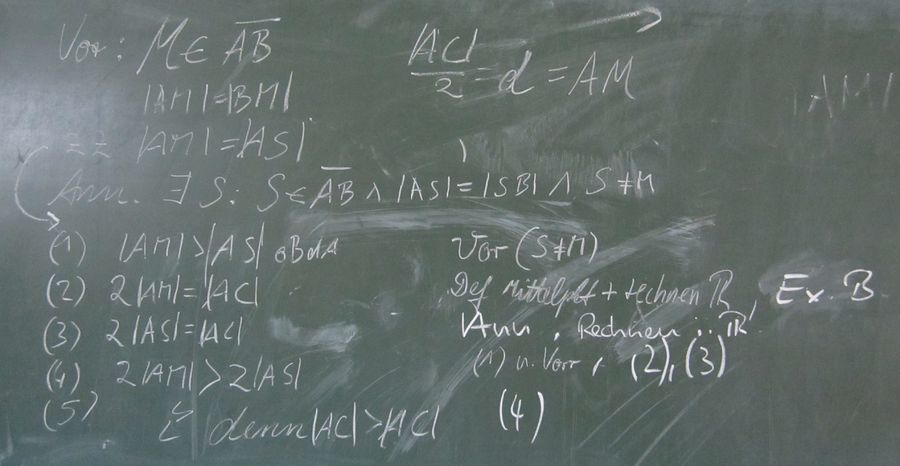
Wenn oben von 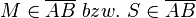$M\in \overline{AB}bzw.S\in \overline{AB}$ dann wird folgend anstelle von B Punkt C verwendet - Namen sind schall und rauch :-)
--Flo60 23:28, 13. Jun. 2012 (CEST)

Dynamische Skizze zur Darstellung von Halbebenen

Bewege den grünen Punkt.

Das einzige 'Problem' das wir hier noch haben ist die Trägergerade g. Sie kann sowohl zu 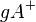$g{A}^{+}$, als auch zu 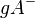$g{A}^{-}$ gehören. Wir sprechen in diesem Zusammenhang von geschlossenen Halbebenen oder einfach nur von Halbebenen. Wenn die Trägergerade nicht Teil der Halbebene ist, dann sprechen wir von offener Halbebenen.
--Flo60 11:51, 13. Jun. 2012 (CEST)

Zurück zur Übersichtsseite

WIKI-Übung-Heckl