23.05.2012: Abstand I und Inzidenz II

Hier ist wie immer Platz für Anregungen und Diskussionen zur heutigen Übungsveranstaltung (23.05.2012)

Hallo zusammen, die Fotos der heutigen Veranstaltung sind online. Ferner habe ich einen direkten Beweisversuch zu Aufgabe 5.5 hochgeladen - dieser steht euch zum kommentieren frei - nutzt auch die Chance.

Lösungsideen Übung Heckl 23.05.2012

Ansonsten wünsch ich eine schöne Exkursionswoche :-).--Flo60 21:56, 23. Mai 2012 (CEST)

Nützliche Videos

Diese (tatsächlich spontan in der Mittagspause auf dem Campusgelände aufgenommenen) Videos könnten zum Verständnis für die Zwischenrelation ganz nützlich sein.
Beide Videos werden auch in der nächsten Woche nochmals hier auf der Übungsseite zu finden sein - spätestens dann machen sie Sinn :-)!

Kommentar zum Video

Hi Flo60,

unsere Cay-Lerngruppe fragt sich, ob wir das Zw(APB) weglassen können?

Unsere Gedanken: Es ist doch egal ob der Punkt P zwischen AB liegt, wenn es außerhalb von AB liegt und somit die Halbgerade AB+ definiert werden kann.

Mit freundlichen Grüßen deine Mutter 13:21, 19. Jun. 2012 (CEST)

---

Hallo 'deine Mutter',
zunächst sei es klug, sich mal gedanken zu machen, wie denn die Halbgerade $\ AB^{+}$ aussehen würde, wenn wir (deinem/eurem Verständnis nach) die Zwischenrelation weglassen?
Gehen wir diesbezüglich sytematisch vor. Wie ist $\ AB^{+}$ definiert?

Definition (Halbgerade AB+): $\left\{ P \in AB | Zw(A, P, B) \ \vee \ Zw(A, B, P)  \right\} \ \cup \ \left\{ {A, B} \right\}$. 

Wenn wir jetzt die erste Zwischenrelation weglassen, dann werden diejenigen Punkte nicht berücksichtig, die auf der 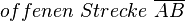$\ offenen \ Strecke \ \overline{AB}$ liegen.
Ich denke, dass euer Verständnis nicht falsch ist - ein Aspekt, den ihr berücksichten müsst ist allerdings, dass wir den Strahl so definieren, dass er aus ALLEN Punkten P (Element AB) besteht für die eine bestimmte Eigenschaft zutrifft (und den Punkten B und A, versteht sich). Es gilt aber NICHT für alle Punkte auf AB. Und die Eigenschaften, die diese Punkte haben müssen, beschreibe ich hier: Nämlich, dass sie zwischen A und B liegen oder derart, dass B zwischen A und P liegt.
Euren Einwand, bzgl. wenn P nicht auf der $\overline{AB}$ kann ich dann weglassen - dieser wurde in der Definition sogar berücksichtigt, nämlich in der logischen Verknüpfung der Zwischenrelationen mit 'oder'. Diese logische Gesamtaussage ist immer dann wahr, wenn eine der beiden Teilaussagen wahr ist - also P ist ein Punkt von AB+, wenn er - wie gesagt, zwischen A und B liegt, oder P derart liegt, dass B zwischen A und P liegt.

Ich hoffe, dass es ein wenig klarer wurde - probierts einfach mal mit farbigen Strahlen aus und sucht euch Punkte auf einem beliebigen Strahl (oder via Geogebra) und schaut, ob er Teil des Strahls (nach Definition) ist, oder nicht. --Flo60 17:09, 19. Jun. 2012 (CEST)

Und das passende Pendant 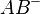$\ AB^{-}$ gleich dazu

--Flo60 21:17, 21. Mai 2012 (CEST)

Zurück zur Übersichtsseite

WIKI-Übung-Heckl