Das Winkelmaß
Was bedeutet es, die Größe eines Winkels zu messen?
| Länge einer Strecke |
Größe eines Winkels
|
| nichtnegative reelle Zahl |
reelle Zahl zwischen 0 und 180
|
Das Winkelmaßaxiom
Axiom IV.1 (Winkelmaßaxiom)
- Zu jedem Winkel
 gibt es genau eine reelle Zahl gibt es genau eine reelle Zahl 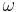 zwischen 0 und 180. zwischen 0 und 180.
Definition V.5: (Größe eines Winkels)
- Die Zahl
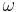 , die entsprechend des Winkelmaßaxioms einem jeden Winkel , die entsprechend des Winkelmaßaxioms einem jeden Winkel  eindeutig zugeordnet werden kann, wird die Größe oder das Maß von eindeutig zugeordnet werden kann, wird die Größe oder das Maß von  genannt. genannt.
In Zeichen: 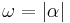 . .
Winkelkonstruktion
Existenz und Eindeutigkeit des Winkelantragens
Axiom IV.2: (Winkelkonstruktionsaxiom)
- Es sei
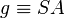 eine Gerade in der Ebene eine Gerade in der Ebene  . Zu jeder reellen Zahl . Zu jeder reellen Zahl 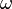 mit mit 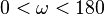 gibt es in jeder der beiden durch gibt es in jeder der beiden durch  bestimmten Halbebenen der Ebene bestimmten Halbebenen der Ebene  genau einen Strahl genau einen Strahl  mit mit 
Winkeladdition
Axiom IV.3: (Winkeladditionsaxiom)
- Wenn der Punkt
 zum Inneren des Winkels zum Inneren des Winkels  gehört , dann gilt gehört , dann gilt 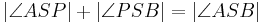 . .
Satz V.2
- Wenn der Punkt
 im Inneren des Winkels im Inneren des Winkels  und nicht auf einem der Schenkel des Winkels und nicht auf einem der Schenkel des Winkels  liegt, dann ist die Größe der beiden Teilwinkel liegt, dann ist die Größe der beiden Teilwinkel 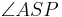 und und 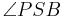 jeweils kleiner als die Größe des Winkels jeweils kleiner als die Größe des Winkels  . .
Beweis von Satz V.2
Vor.: im inneren im inneren
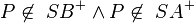
Beh.: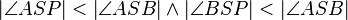
Versuchen Sie es selbst!
Rechte Winkel
Definition V.6 : (Rechter Winkel)
- Wenn ein Winkel die selbe Größe wie einer seiner Nebenwinkel hat, so ist er ein rechter Winkel.
Definition V.7 : (Supplementärwinkel)
- Zwei Winkel heißen supplementär, wenn die Summe ihrer Größen 180 beträgt.
Axiom IV.4: (Supplementaxiom)
- Nebenwinkel sind supplementär.
Satz V.3 : (Existenz von rechten Winkeln)
- Wenn ein Winkel die Größe 90 hat, dann ist er ein rechter Winkel.
Beweis von Satz V.3
Das können Sie selbst!
Satz V.4 :
- Jeder rechte Winkel hat das Maß 90.
Beweis von Satz V.4 :
- Das können Sie selbst!
Die Relation Senkrecht auf der Menge der Geraden
Definition V.8 : (Relation senkrecht auf der Menge der Geraden)
- Es seien
 und und  zwei Geraden. Wenn sich zwei Geraden. Wenn sich  und und  schneiden und bei diesem Schnitt rechte Winkel entstehen, dann stehen die Geraden schneiden und bei diesem Schnitt rechte Winkel entstehen, dann stehen die Geraden  und und  senkrecht aufeinader. senkrecht aufeinader.
- In Zeichen:
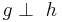 (in der Formelbeschreibungssprache Tex: \perp , läßt sich gut merken, von perpendicular) (in der Formelbeschreibungssprache Tex: \perp , läßt sich gut merken, von perpendicular)
Bemerkung: Testen Sie ob die Definition korrekt ist: Warum muss nicht gefordert werden, dass die beiden Geraden komplanar sind?
Definition V.9 : (noch mehr Senkrecht)
- Eine Gerade
 und eine Strecke und eine Strecke  stehen senkrecht aufeinander, wenn die stehen senkrecht aufeinander, wenn die  und die Gerade und die Gerade  senkrecht aufeinander stehen. senkrecht aufeinander stehen.
Ergänzen Sie:
Eigenschaften der Relation senkrecht
Satz V.5: (Existenz und Eindeutigkeit der Senkrechten zu einer Geraden auf einem Punkt dieser Geraden)
- Es sei
 eine Gerade der Ebene eine Gerade der Ebene  . Ferner sei . Ferner sei  ein Punkt auf ein Punkt auf  . In der Ebene . In der Ebene  gibt es genau eine Gerade gibt es genau eine Gerade 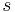 , die durch , die durch  geht und senkrecht auf geht und senkrecht auf  steht. steht.
Beweis von Satz V.5
Übung
|
 gibt es genau eine reelle Zahl
gibt es genau eine reelle Zahl 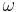 zwischen 0 und 180.
zwischen 0 und 180.
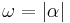 .
.
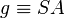 eine Gerade in der Ebene
eine Gerade in der Ebene  . Zu jeder reellen Zahl
. Zu jeder reellen Zahl 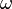 mit
mit 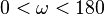 gibt es in jeder der beiden durch
gibt es in jeder der beiden durch  bestimmten Halbebenen der Ebene
bestimmten Halbebenen der Ebene 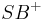 mit
mit 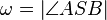
 zum Inneren des Winkels
zum Inneren des Winkels  gehört , dann gilt
gehört , dann gilt 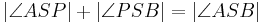 .
.
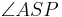 und
und 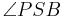 jeweils kleiner als die Größe des Winkels
jeweils kleiner als die Größe des Winkels  im inneren
im inneren
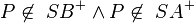
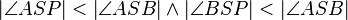
 und
und  zwei Geraden. Wenn sich
zwei Geraden. Wenn sich 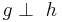 (in der Formelbeschreibungssprache Tex: \perp , läßt sich gut merken, von perpendicular)
(in der Formelbeschreibungssprache Tex: \perp , läßt sich gut merken, von perpendicular)
 stehen senkrecht aufeinander, wenn die
stehen senkrecht aufeinander, wenn die  senkrecht aufeinander stehen.
senkrecht aufeinander stehen. . Ferner sei
. Ferner sei 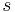 , die durch
, die durch 
