Beschreibung und Einsatz des DGS

Was ist funktionales Denken?

Sallop ausgedrückt versteht man unter funktionalem Denken das Denken in Zusammenhängen und Abhängigkeiten. Dies klingt zunächst einleuchtend, wenn wir aber von einem Funktionsbegriff ausgehen, der sich als linkstotale und rechtseindeutige Relation, also Teilmenge aus einem Kreuzprodukt 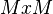$M x M$ versteht haben wir ein Problem.
Aus diesem Grunde müssen wir zunächst von einem anderen Verständnis von Funktionen ausgehen.

„Funktionen drücken Beziehungen zwischen Zahlen und zwischen Größen aus.“ (Vollrath& Weigand (2007): Algebra in der Sekundarstufe, 131)

Dies bringt uns der Sache nämlich schon ein ganzes Stück näher, auch wenn diese Definition oder viel mehr Beschreibung doch sehr populärwissenschaftlich anmutet.
Um nun zu erkennen, was funktionales Denken genau ist, betrachten wir die Unterteilung dessen nach Vollrath:

Zuordnungscharakter bzw. -eigenschaft

Einer Eingangsgröße wird immer eine Ausgangsgröße zugeordnet. Somit werden Zusammenhänge beschrieben. Dabei ist jeweils eine Größe abhängig von der anderen.
$Formal: \ Seien \ M_1 \ und \ M_2 \ zwei \ Mengen. \ \forall x \ \in \ M_1: \ x \rightarrow f(x)$

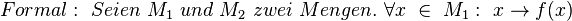
Änderungsverhalten bzw. Kovariation

Mittels Funktionen kann man erfassen, wie sich die Veränderung einer Größe auf die andere auswirkt.
z. B. die Additivität der Proportionalität: 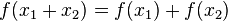$f(x_1 + x_2) = f(x_1) + f(x_2)$

Betrachtung als Ganzes bzw. Sicht als Ganzes

Mittels Funktionen kann ein Sachverhalt als ganzes Betrachtet werden. Dazu dient in erster Linie der Graph.

All diese Aspekte sind grundlegend für das funktionale Denken. Dass nicht nur die Kovariation Aspekt des funktionalen Denkens sei folgend an einem 'Klassiker' begründet:
(Siehe: Einsatz der DGS)

Zurück zur Hauptseite Didaktik 8-10 WiSe 2011/12

Didaktik 08 - 10