Beweis Versuch Nummer 1 Serie 08 a 2
Ich nehme Bezug auf den Apfel und das darin eingezeichnete reg. Fünfeck. In jedem regelmäßigen n-Eck gilt, dass die Innenwinkelsumme an jedem Eck gleich ist - (Begründung: trivial).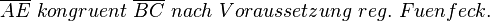 
Wir machen es uns nun einfacher und bestimmen den Mittelpunkt der Strecke 
. Sei dieser M. Wenn wir nun die Mittelsenkrechte eintragen können wir zeigen, dass das Dreieck 
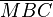auf das Dreieck 
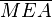gespiegelt werden kann. Ich glaube es müsste aber noch einfacher gehen, seis drum. Begründungen sind Punkte A und B, sowie der Fixpunkt M und die beiden treuen Innenwinkel. Aufgrund der Spiegelunsdefinition existiert nun eine Senkrechte CE, die nach der Umkehrung des Stufenwinkelsatzes parallel zur Geraden AB ist. Für andere Diagonalen geht man analog vor, dies war o. B. d. A.
Hier doch noch eine Skizze:
Jetzt aber zum eigentlichen Beweis. Auch hier gilt wieder oBdA. Aber hier gibt es zunächst die Skizze, sonst verenne ich mich wieder.
Um dies zu zeigen, muss nun gezeigt werden, dass A an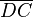 
gespiegelt wurde. Mit dem Prinzip des Ausfallwinkel gleich Einfallwinkel sollte uns das ohne Probleme gelingen: Geht nicht!
VIEL EINFACHER: Ich habe vorher ja so ungefähr bewiesen, dass die Seiten eine parallele Diagonale haben und zwar diejenige, deren Endpunkte nicht durch die Mittelsenkrechte der Seite gehen. Im Falle meiner Seite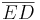 
ist dies die Diagonale 
. Nun gilt: Fehler beim Parsen(Lexikalischer Fehler): \overline{DF} \ || \ \overline{AC} \ und \ weil \ AD \ und BC \ ebenfalls \ parallel \ sind \ ist \overline{ACFD} \ ein \ Parallelogramm \ in \ dem \ gegenüberliegende \ Seiten \ logischerweise \ gleich \ lang \ sind \ und \ daraus \ folgt: \overline{AC} \tilde {=} \overline{DF}
FERTIG!--Flo60 18:53, 18. Jan. 2012 (CET)
