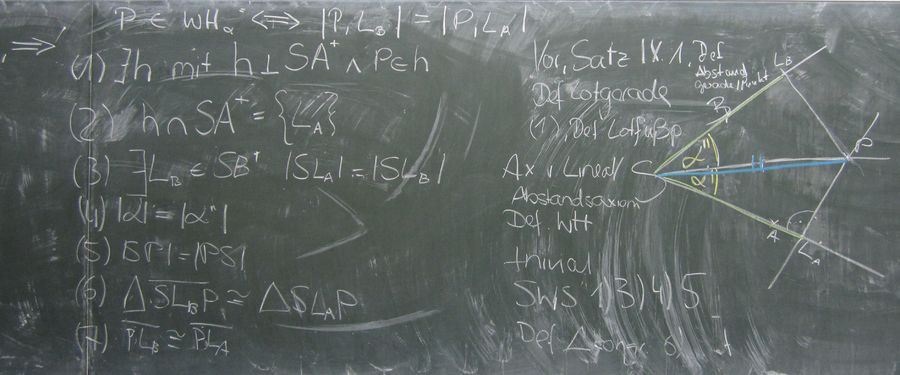Beweisideen Übung Heckl - Übung 12 (SoSe2012)

Absolute Geometrie

Aufgabe 12.1

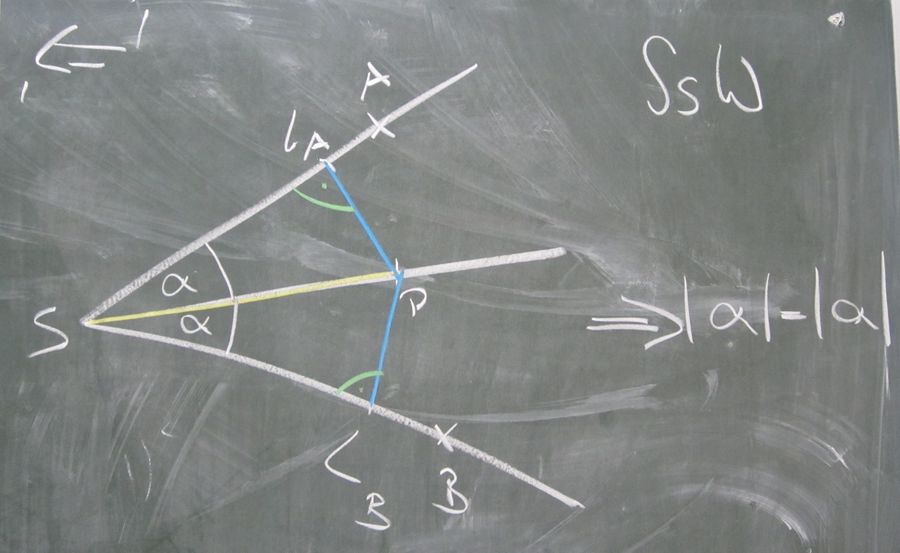
Man beweise: Ein Punkt $\ P$ gehört genau dann zur Winkelhalbierenden des Winkels $\ \alpha$, wenn er zu den Schenkeln von $\ \alpha$ jeweils denselben Abstand hat.

'=>'

Grundlegende Beweisidee '<='

Aufgabe 12.2

Beweisen Sie die Umkehrung des Wechselwinkelsatzes
a) mithilfe der Umkehrung des Stufenwinkelsatzes.
b) ohne die Umkehrung des Stufenwinkelsatzes zu verwenden.

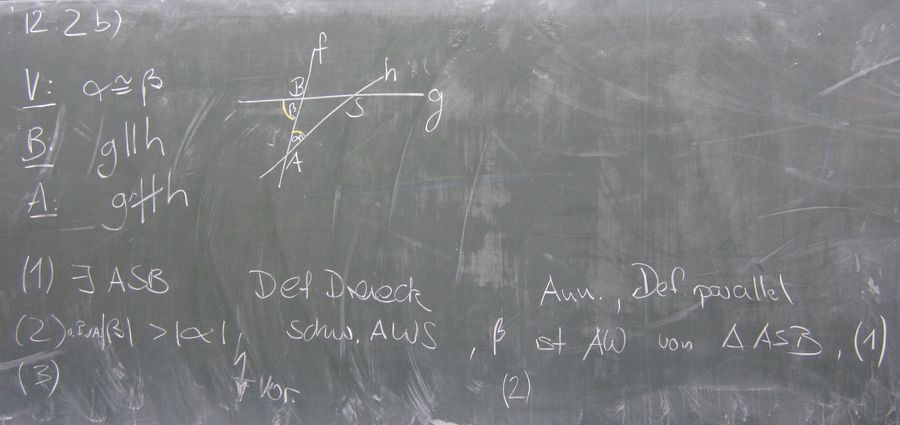
Aufgabe 12.3

Beweisen Sie: Wenn $\ P$ ein Punkt außerhalb der Geraden $\ g$ ist, dann gibt es eine Gerade $\ h$, die durch $\ P$ geht und parellel zu $\ g$ ist.

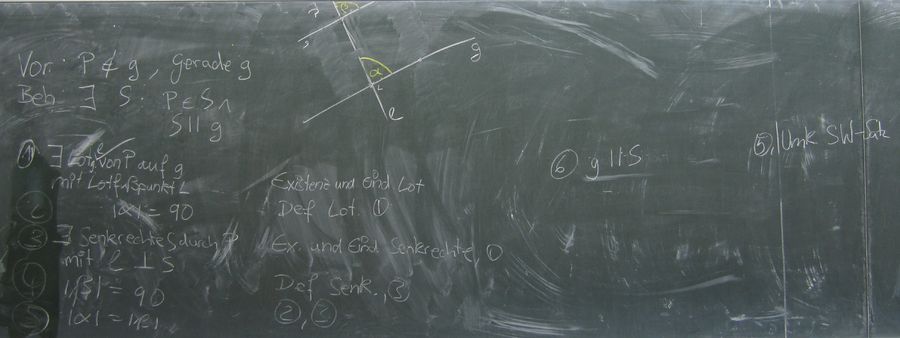
Euklidische Geometrie

Aufgabe 12.8

Beweisen Sie den starken Außenwinkelsatz.

Diesen Beweis haben wir ikonisch geführt. Dabei wurden auf die Verwendungen von Variablen verzichtet. Stattdessen wurde (didaktisch sinnvoll) mit Farben gearbeitet. Die Begründung ist lückenhaft - darauf kam es uns in diesem Beweis aber nicht an - entscheidend war die Nutzung der Farben und der dadurch womöglich entstehenden besseren Übersichtlichkeit.

Zurück zur Übersichtsseite

Übung_Aufgaben_12_S (SoSe_12)