Beziehungen zwischen Seitenlängen und Innenwinkelgrößen von Dreiecken SoSe 12
Inhaltsverzeichnis[Verbergen] |
Satz XIV.1: (Der größeren Seite liegt der größere Winkel gegenüber)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen.
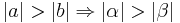
- Es sei
Beweis von Satz XIV.1
Es sei  ein Dreieck.
ein Dreieck.
Voraussetzung:
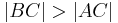 bzw.
bzw. 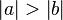
Behauptung:
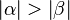
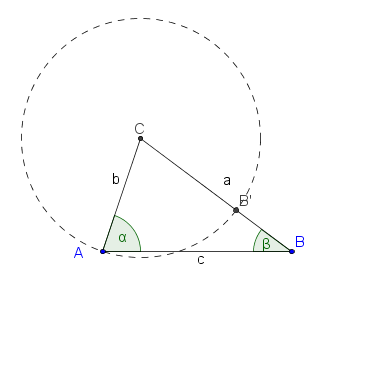
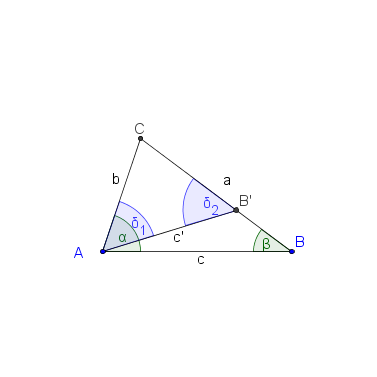
Die folgenden Hilfskonstruktionen liefern die Beweisidee (kommentieren Sie die Abbildungen und führen Sie den Beweis):
stimmt das so?
Wir führen einen Widerspruchsbeweis, indem wir annehmen: alpha = beta
(1) | |=|
|=| | (Ann.)
| (Ann.)
(2) |a| = |b| (1) , (Basiswinkelsatz)
(3) Widerspruch zur Vor. Ann. ist zu verwerfen, Beh. stimmt --Die Drei ??? 10:59, 14. Jul. 2012 (CEST)
Ihre Annahme ist zu kurz gegriffen - warum?--Schnirch 13:00, 16. Jul. 2012 (CEST)
Vielleicht kann es so funktionieren:
1. Zeichne einen Kreis um C mir Radius: CA (Konstruktion)
2. CB geschnitten k= B´ (1. Konstruktion)
3. CA=CB`daraus folgt Gamma 1=Gamma2 (Hinrichtung BWS)
4. Gamma 2 ist größer als Beta (schwacher Außenwinkelsatz, Dreieck AB´B)
5. Gamma 1 + Delta= Alpha (Winkeladdition)
6. Beta ist kleiner als Alpha (5.4.3)--Geogeogeo 17:03, 16. Jul. 2012 (CEST)
Satz XIV.2: (Dem größeren Winkel liegt die größere Seite gegenüber)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen. 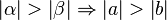
- Es sei
Beweis von Satz XIV.2
Zusatzaufaufgabe