Beziehungen zwischen den Seitenlängen und den Innenwinkelgrößen eines Dreiecks (SoSe 11)
Inhaltsverzeichnis[Verbergen] |
Satz IX.2: (Der größeren Seite liegt der größere Winkel gegenüber)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen.
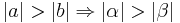
- Es sei
Beweis von Satz IX.2
Es sei  ein Dreieck.
ein Dreieck.
Voraussetzung:
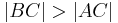 bzw.
bzw. 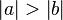
Behauptung:
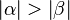
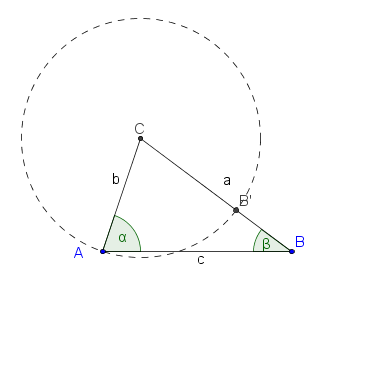
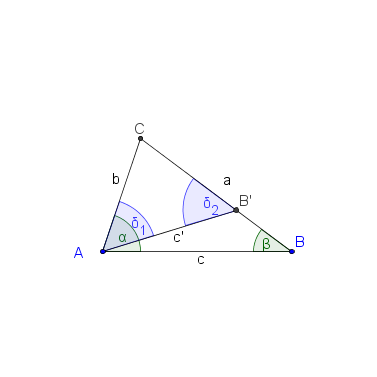
Die folgenden Hilfskonstruktionen liefern die Beweisidee (kommentieren Sie die Abbildungen und führen Sie den Beweis):
1. Konstruiere B' für das gilt CB'(Strecke)= AC(Strecke) und B' Element CB(Strecke) (Axiom vom Lineal)
2. Das Dreieck AB'C ist nun ein gleichschenkliges (1.; Def. gleichschenkliges Dreieck)
3. δ1=δ2 (Basiswinkelsatz; 2.)
4. δ1=δ2 sind jeweils kleiner als 90 (3.;Korollar 2)
5. α ist größer als δ1 (B' liegt nach Konstruktion im Inneren, Winkeladditionsax.)6. δ2 ist Außenwinkel von dem Winkel AB'B (nach Konstruktion(?))
7. β ist kleiner als δ2 (6.; schwacher Außenwinkelsatz)
8. Somit ist α größer β (3; 5.;7.)
Nun muss noch bewiesen werden, dass γ kleiner ist als α
--Verteidigungswolf
Danke für deinen Beweis. Ein paar kleine Anmerkungen.
Zu Schritt 1: Was steht im Axiom vom Lineal und wann darf man es genau genommen wie anwenden?
Begründung in Schritt 8 habe ich ergänzt.
Wozu schreibst du Schritt 4?
Warum muss noch bewiesen werden, dass γ kleiner ist als α ist?--Tutorin Anne 22:31, 14. Jul. 2011 (CEST)
Satz IX.3: (Dem größeren Winkel liegt die größere Seite gegenüber)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen. 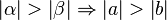
- Es sei
Beweis von Satz IX.3
Übungsaufgabe
Hier, weil die Tutaufgabe von Woche 14 keine bearbeitbare Wikiseite hat. Falls nicht okay, bitte verschieben.
Voraussetzung: Alpha ist kleiner als Beta
Behauptung: Dann auch Seite a kleiner als Seite b
Annahme (für Widerspruchsbeweis): Nö, Seite a ist nicht kleiner als Seite b
Fallunterscheidung
1. Seite a gleich Seite b -> dann haben wir ein gleichschenkliges Dreieck mit Alpha gleich Beta und ...
widersprechen dadurch der Voraussetzung
2. Seite a größer als Seite b. Daraus folgt aber (wie wir kurz zuvor bewiesen haben), dass dann Alpha größer als Beta sein muss...
was schon wieder der Voraussetzung widerspricht.
Und da mehr Fälle nicht auftreten können, sollte das doch schon reichen, oder? Die Annahme ist zu verwerfen, die ursprünglche Behauptung muss gelten.
Normalerweise wäre mir das zu knapp, um die Umkehrung von "Aus A folgt B" zu beweisen, das B ja oft aus allen möglichen Konstellationen hervorgehen kann und A nicht unbedingt der Verursacher von B sein muss, wenn halt mal B eingetreten ist (die oft zitierte nasse Straße).
Hier aber ist "Aus A folgt B" schon sehr eng, denn der größere Winkel, der bewiesenermaßen der größeren Seite gegenüberliegt, kann (aus der Konstruktion eines Dreiecks bzw. eines Winkels) eben nicht auch noch einer anderen Seiten gegenüberliegen. Versteht jemand, was ich meine? Und liege ich richtig?--WikiNutzer 14:42, 25. Jul. 2011 (CEST)