Bin ich für die Klausur fit? SS12
Es ist bekannt, dass Auswendiglernen nicht so wirklich viel nutzt für die Klausur (egal ob alte oder neue Prüfungsordnung).
Hier drei Aufgaben, mit denen Sie testen können ob Sie bezüglich des Transfers Ihres Wissens fit genug für die Klausur sind:
Testaufgabe 01: Definieren
Scherenwagenheber lassen sich aus rein geometrischer Sicht auf Rauten zurückführen. Aus rein geometrischer Sicht könnten aber auch Drachen und weitere Vierecke Scherenwagenhebern zugrunde liegen.
Die folgende Applikation zeigt prinzipiell mögliche Scherenwagenhebervierecke:
Hinweis: Die Punkte 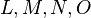 können bewegt werden.
können bewegt werden.
Definieren Sie den Begriff gemeines Scherenwagenheberviereck.
Sie sollten in der Lage sein, die entscheidende Gemeinsamkeit aller möglichen Vierecke 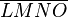 zu erkennen und diese definierende Eigenschaft in einer formal korrekten Definition zu verwenden.
zu erkennen und diese definierende Eigenschaft in einer formal korrekten Definition zu verwenden.
Testaufgabe 02
Wir gehen von folgender Definition aus:
Definition
Raute
Eine Raute ist ein Viereck dessen Seiten alle dieselbe Länge haben.
Nur unter Verwendung der Dreieckskongruenzsätze, obiger Definition, der Definition senkrecht auf der Menge der Geraden bzw. Strecken, der Definition Nebenwinkel und der Definition Rechter Winkel sollten Sie jetzt die folgende Beweisaufgabe lösen können:
- Beweisen Sie: Jeder Drachen ist ein Scherenwagenheberviereck.
Sie sollten diese Aufgabe jetzt völlig allein und ohne jede Hilfe lösen können. Die Aufgabe ist von geringem Schwierigkeitsgrad. Sie sollten nicht mehr als 10 Minuten für den Beweis benötigen.
Hinweis: Dass sich die Diagonalen einer Raute schneiden, müssen Sie nicht nachweisen.
Testaufgabe 03
Es sei  ein Dreieck mit den schulüblichen Bezeichnungen. Ferner seien
ein Dreieck mit den schulüblichen Bezeichnungen. Ferner seien 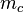 und
und 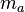 die Mittelsenkrechten der Seiten
die Mittelsenkrechten der Seiten  bzw.
bzw.  des Dreiecks
des Dreiecks  . Diese Mittelsenkrechten mögen sich in dem Punkt
. Diese Mittelsenkrechten mögen sich in dem Punkt  schneiden. Beweisen Sie, dass auch die Mittelsenkrechte
schneiden. Beweisen Sie, dass auch die Mittelsenkrechte 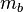 der Seite
der Seite  von
von  durch
durch  geht.
geht.
Sie sollten völlig ohne Hilfe selbständig auf den Beweis kommen. Das kann je nach Tagesform und erster Idee momentan (14 Tage vor der Klausur) länger dauern. Nach zwei Tagen spätestens müssten Sie die Lösung gefunden haben.
Hinweis: Dass sich 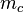 und
und 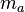 schneiden müssen Sie nicht zeigen.
schneiden müssen Sie nicht zeigen.

