Der Basiswinkelsatz WS 20 21
Aus Geometrie-Wiki
Inhaltsverzeichnis |
Der Basiswinkelsatz
Gleichschenklige Dreiecke
Definition VIII.1 : (gleichschenkliges Dreieck)
...
Der Basiswinkelsatz
Satz VIII.1: (Basiswinkelsatz)
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
Beweis:
Voraussetzung: Dreieck ist gleichschenklig
Behauptung: Basiswinkel sind kongruent
| Nr. | Skizze | Beweisschritt | Begründung |
|---|---|---|---|
| (1) | 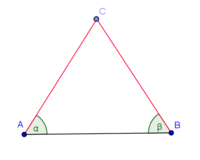
|
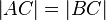
|
|
| (2) | 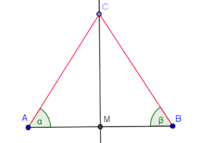
|
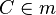 mit mit  ist Mittelsenkrechte von ist Mittelsenkrechte von 
|
|
| (3) | |
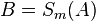
|
|
| (4) | |
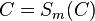
|
|
| (5) | |
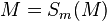
|
|
| (6a) | |
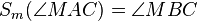
|
|
| (6b) | |
|

