Der Basiswinkelsatz WS 23 24
Aus Geometrie-Wiki
Inhaltsverzeichnis |
Der Basiswinkelsatz
Gleichschenklige Dreiecke
Definition VIII.1 : (gleichschenkliges Dreieck)
Ein Dreieck mit zwei zueinander kongruenten Seiten heißt gleichschenkliges Dreieck. Die beiden zueinander kongruenten Seiten heißen Schenkel, die dritte Seite heißt Basis des Dreiecks und die Innenwinkel an der Basis heißen Basiswinkel.
Der Basiswinkelsatz
Satz VIII.1: (Basiswinkelsatz)
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
Beweis:
Voraussetzung: Dreieck ist gleichschenklig
Behauptung: Basiswinkel sind kongruent
| Nr. | Skizze | Beweisschritt | Begründung | |
|---|---|---|---|---|
| (1) | 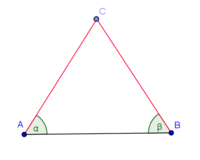
|
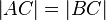
|
||
| (2) | 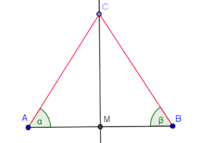
|
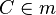 mit mit  ist Mittelsenkrechte von ist Mittelsenkrechte von 
|
||
| (3) | |
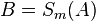
|
||
| (4) | |
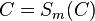
|
||
| (5) | |
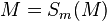
|
||
| (6a) | |
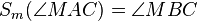
|
||
| (6b) | |
|

