Der Inkreis und die Winkelhalbierenden eines Dreiecks (WS10/11)

Winkelhalbierenden eines Dreiecks

Definition XV.1 : (Winkelhalbierenden eines Dreiecks)

Unter den Winkelhalbierenden eines Dreiecks versteht man die Winkelhalbierenden der Innenwinkel des Dreiecks.

Satz XV.1a : (Abstand eines Punktes einer Winkelhalbierenden zu den Schenkeln des Winkels)

Jeder Punkt der Winkelhalbierenden eines Winkels hat zu den Schenkeln des Winkels jeweils ein und denselben Abstand.

Satz XV.1b : (Umkehrung von Satz XV.1a)

(das können Sie selbst:)

Hat ein Punkt zu den Schenkeln des Winkels jeweils ein und denselben Abstand, so ist er ein Punkt der Winkelhalbierenden des Winkels.--Jbo-sax 10:26, 29. Jan. 2011 (UTC)

wir sollten noch voraussetzen, dass der zu betrachtende Punkt im Inneren des Winkels liegt!--Schnirch 10:53, 4. Feb. 2011 (UTC)

Winkelhalbierendenkriterium

(auch das sollten Sie jetzt selbst hinbekommen:)

Genau dann wenn ein Punkt zu den Schenkeln des Winkels jeweils ein und denselben Abstand hat, ist er ein Punkt der Winkelhalbierenden des Winkels.--Jbo-sax 10:29, 29. Jan. 2011 (UTC)

auch hier noch einfügen: wenn ein Punkt im Inneren eines Winkels...--Schnirch 11:07, 4. Feb. 2011 (UTC)

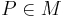Eine Menge an Punkten M ist genau dann Winkelhalbierende des Winkels $\angle ASB$, wenn jeder Punkt $P \in M$ ein und denselben Abstand zu den Schenkeln des Winkels $\angle ASB$ hat.--Engel82 12:52, 30. Jan. 2011 (UTC) Beweis siehe Übungsaufgabe

diese Formulierung gefällt mir nicht so, versuchen Sie mal aus ihrem Kriterium wieder zwei
 Sätze zu machen, dann merken Sie dass die Formulierung nicht korrekt ist.--Schnirch 11:07, 4. Feb. 2011 (UTC)

Satz XV.2 : (Schnittpunkt der Winkelhalbierenden eines Dreiecks)

Die Winkelhalbierenden eines Dreiecks schneiden sich in genau einem Punkt.

Beweis von Satz XV.2 mit Hilfe des Winkelhalbierendenkriteriums: Versuchen Sie es selbst:

Inkreis eines Dreiecks

Definition XV.2 : (Tangente an einen Kreis)

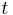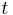Eine Gerade $\ t$ berührt einen Kreis $\ k$, wenn sie mit dem Kreis $\ k$ genau einen Punkt $\ P$ gemeinsam hat. Die Gerade $\ t$ heißt Tangente im Punkt $\ P$.

Definition XV.3 : (Strecke berührt Kreis)

Eine Strecke $\overline{AB}$ berührt einen Kreis $\ k$, wenn sie... (ergänzen Sie!)

...wenn sie eine Teilmenge der Tangente t des Kreises ist.--Jbo-sax 09:38, 29. Jan. 2011 (UTC)

Definition XV.4 : (Inkreis eines Dreiecks)

Ein Kreis, der alle drei Seiten eines Dreiecks in jeweils genau einem Punkt berührt, heißt Inkreis des Dreiecks.

Satz XV.3 : (Existenz und Eindeutigkeit des Inkreises)

...ergänzen Sie!

Es gibt genau einen Inkreis des Dreiecks für den gilt, dass er alle Seiten des Dreiecks in jeweils genau einem Punkt berührt.--Jbo-sax 10:34, 29. Jan. 2011 (UTC)

den zweiten Teil des Satzes brauchen Sie nicht mehr, da der Begriff Inkreis ja schon definiert
 wurde. Bessere Formulierung: Jedes Dreieck besitzt genau einen Inkreis.--Schnirch 11:08, 4. Feb. 2011 (UTC)