Der Schwerpunkt und die Seitenhalbierenden eines Dreiecks WS 11/12
Die Fotos demonstrieren, was unter dem Schwerpunkt eines Dreiecks zu verstehen ist. Erstellen Sie das Skript selbst.

|

|
|---|---|

|

|

|

|
Seitenhalbierende eines Dreiecks
Definition XVI.1 (Seitenhalbierende eines Dreiecks)
In einem Dreieck sind die Strecken von einem Eckpunkt zu dem Mittelpunkt der, dem jeweiligen Eckpunkt gegenüberliegenden Seite des Dreiecks "Seitenhalbierende eines Dreiecks".
Oder etwas ausführlicher:
Es sei  ein Dreieck.
ein Dreieck.
Unter der Seitenhalbierende des Dreiecks  der Seite
der Seite  versteht man die Strecke
versteht man die Strecke 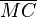 , wobei M der Mittelpunkt der Strecke
, wobei M der Mittelpunkt der Strecke  ist.
ist.
Unter der Seitenhalbierende des Dreiecks  der Seite
der Seite  versteht man die Strecke
versteht man die Strecke 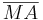 , wobei M der Mittelpunkt der Strecke
, wobei M der Mittelpunkt der Strecke  ist.
ist.
Unter der Seitenhalbierende des Dreiecks  der Seite
der Seite  versteht man die Strecke
versteht man die Strecke  , wobei M der Mittelpunkt der Strecke
, wobei M der Mittelpunkt der Strecke  ist.
ist.
--Flobold 18:24, 31. Jan. 2012 (CET)
Satz XVI.1: (Existenz und Eindeutigkeit der Seitenhalbierenden)
In einem Dreieck existiert zu jeder Seite des Dreiecks genau eine Seitenhalbierende. --Flobold 18:24, 31. Jan. 2012 (CET)
Schwerpunkt eines Dreiecks
Satz XVI.2: (Schnittpunkt der Seitenhalbierenden eines Dreiecks)
Die Seitenhalbierenden eines Dreiecks schneiden einander in genau einem Punkt.--Flobold 18:27, 31. Jan. 2012 (CET)
Definition XVI.2 (Schwerpunkt eines Dreiecks)
Der Schnittpunkt der Seitenhalbierenden eines Dreiecks heißt Schwerpunkt eines Dreiecks. --Flobold 18:27, 31. Jan. 2012 (CET)

