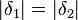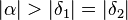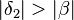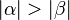|
Satz IX.2: (Der größeren Seite liegt der größere Winkel gegenüber)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen. ein Dreieck mit den schulüblichen Bezeichnungen.
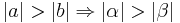
Beweis von Satz IX.2
Es sei  ein Dreieck. ein Dreieck.
Voraussetzung:
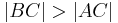 bzw. bzw. 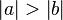
Behauptung:
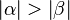
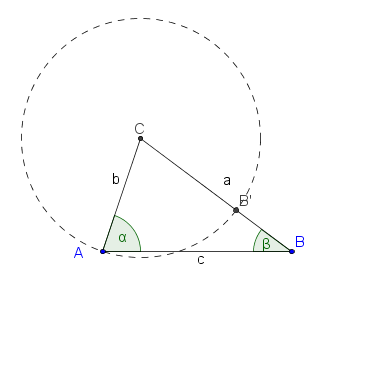
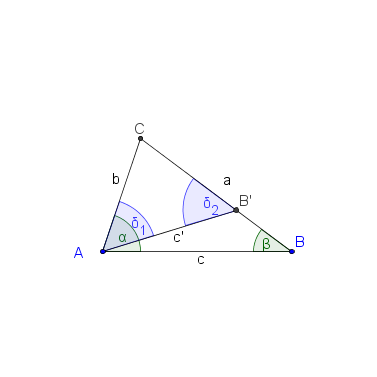
Die folgenden Hilfskonstruktionen liefern die Beweisidee (kommentieren Sie die Abbildungen und führen Sie den Beweis):
 |
|
| Skizze 1 |
Skizze 2
|
Satz IX.3: (Dem größeren Winkel liegt die größere Seite gegenüber)
- Es sei
 ein Dreieck mit den schulüblichen Bezeichnungen. ein Dreieck mit den schulüblichen Bezeichnungen.
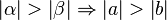
Beweis von Satz IX.3
Übungsaufgabe
Beweis von Caro44

--Caro44 11:21, 26. Jan. 2013 (CET)
Kommentar --*m.g.* 17:35, 26. Jan. 2013 (CET)
- Schritt 3 brauchen Sie nicht: Wir messen den Abstand
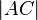 und tragen ihn auf und tragen ihn auf 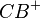 ab. ab.
- Schritt 6 wird ebenso nicht benötigt, Es ist zwar richtig, dass jede Strecke zu sich selbst kongruent ist, da wir aber nicht mit den Dreieckskongruenzsätzen arbeiten brauchen wir eine derartige Feststellung kaum.
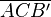 ist bereits nur entsprechend Schritt 5 gleichschenklig. ist bereits nur entsprechend Schritt 5 gleichschenklig.
- Die weitere Beweisführung sollte ohne den starken Außenwinkelsatz gehen. Die Seiten-Winkel_Beziehungen gelten bereits in der absoluten Geometrie.
Beweis mit Lücken zur Ergänzung
Wir beziehen uns auf die Skizzen 1 bzw. 2.
| Nr. |
Beweischritt |
Begründung
|
| (I) |
Auf 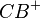 existiert ein Punkt existiert ein Punkt 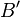 , der zu , der zu  den Abstand der Länge den Abstand der Länge 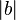 der Strecke b hat. der Strecke b hat. |
Axiom vom Lineal
|
| (II) |
Das Dreieck 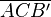 ist gleichschenklig, wobei ist gleichschenklig, wobei  und und 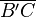 die zueinender kongruenten Seiten sind. die zueinender kongruenten Seiten sind. |
(I)
|
| (III) |
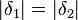 |
(II), Basiswinkelsatz
|
| (IV) |
Zw(CB'B) |
Vor, (I)
|
| (V) |
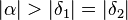 |
Winkeladditionsaxiom
|
| (VI) |
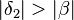 |
schwacher Außenwinkelsatz
|
| (VII) |
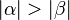 |
(V), (VI)
|
|
--*m.g.* 19:35, 3. Feb. 2013 (CET)
(IV) mit Definition Zwischen zu begründen, passt nicht. Sie müssten begründen, warum die Forderungen der Definition erfüllt sind. (I) ist schon mal gut, reicht aber nicht ganz. Tipp: Voraussetzungen
Dann gilt Zw(CB'B) aufgrund der Voraussetzung
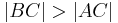
und Schritt (I).
--
Natürliches Mineralwasser 11:42, 4. Feb. 2013 (CET)
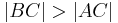 und Schritt (I).
und Schritt (I). ein Dreieck mit den schulüblichen Bezeichnungen.
ein Dreieck mit den schulüblichen Bezeichnungen. 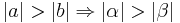
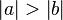
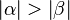


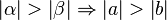

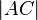 und tragen ihn auf
und tragen ihn auf 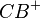 ab.
ab.
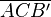 ist bereits nur entsprechend Schritt 5 gleichschenklig.
ist bereits nur entsprechend Schritt 5 gleichschenklig.
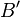 , der zu
, der zu  den Abstand der Länge
den Abstand der Länge 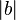 der Strecke b hat.
der Strecke b hat.  und
und 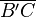 die zueinender kongruenten Seiten sind.
die zueinender kongruenten Seiten sind.