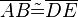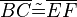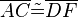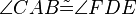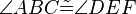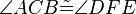Die Kongruenzrelation, Geradenspiegelung als Kongruenzabbildung WS 13/14
Inhaltsverzeichnis[Verbergen] |
Streckenkongruenz
Definition VII.1: (Streckenkongruenz)
- Zwei Strecken sind kongruent, wenn sie dieselbe Länge haben.
- In Zeichen
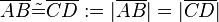
- Zwei Strecken sind kongruent, wenn sie dieselbe Länge haben.
Satz VII.1:
- Die Relation kongruent ist auf der Menge aller Strecken eine Äquivalenzrelation.
Der Beweis ergibt sich unmittelbar durch Rückführung auf die Gleicheitsrelation auf der Menge der reellen Zahlen.
Aufgrund der Strecken- und Längentreue der Geradenspiegelung sind Strecken und ihre bei einer Geradenspiegelung entstehenden Bildstrecken kongruent zueinander.
Winkelkongruenz
Analog zum Begriff der Streckenkongruenz sollen zwei Winkel genau dann kongruent zueinander genannt werden, wenn sie dieselbe Größe haben.
Definition VII.2 : (Winkelkongruenz)
- Zwei Winkel die dieselbe Größe haben heißen kongruent zueinander.
- In Zeichen:
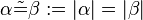
- Zwei Winkel die dieselbe Größe haben heißen kongruent zueinander.
Satz VII.2:
- Die Relation kongruent ist auf der Menge aller Winkel eine Äquivalenzrelation.
Der Beweis ergibt sich unmittelbar durch Rückführung auf die Gleicheitsrelation auf der Menge der reellen Zahlen.
Aufgrund der Winkeltreue der Geradenspiegelung und der Eigenschaft winkelmaßerhaltend zu sein, sind Winkel und ihre bei einer Geradenspiegelung entstehenden Bilder kongruent zueinander.
Dreieckskongruenz
In der Schule spricht man häufig davon, dass zwei Dreiecke dann kongruent zueinander sind, wenn sie in allen Stücken übereinstimmen. Unter den Stücken eines Dreieck sind dabei die jeweils drei Seiten und die jeweils drei Innenwinkel zu verstehen.
Definition VII.3: (Dreieckskongruenz)
- Wenn für zwei Dreiecke
 und
und  die folgenden 6 Kongruenzen
die folgenden 6 Kongruenzen
- Wenn für zwei Dreiecke
- gelten,
- dann sind die beiden Dreiecke
 und
und  kongruent zueinander.
kongruent zueinander.
Satz VII.3:
- Die Relation kongruent ist auf der Menge aller Dreiecke eine Äquivalenzrelation.
Der Beweis ergibt sich unmittelbar durch Rückführung auf die Gleicheitsrelation auf der Menge der reellen Zahlen.
Satz VII.4:
Bei einer Geradenspiegelung sind ein Dreieck und sein Bilddreieck kongruent zueinander.
Beweis: ergibt sich unmittelbar aus der Winkel- und Streckenkongruenz der Geradenspiegelung und der Definition Dreieckskongruenz.