Die Kongruenzsätze SoSe 12
Die Kongruenzsätze
Wir haben im Abschnitt über die Kongruenzrelation die Definition Dreieckskongruenz kennengelernt. Ein Dreieck ist dann kongruent zu einem anderen Dreieck, wenn es in allen seinen "Stücken" (Seiten und Winkel) übereinstimmt, d.h. die Stücke jeweils kongruent zueinander sind. Wir werden jetzt sehen, dass die Kongruenz von zwei Dreiecken bereits sichergestellt sein kann, wenn diese in drei Stücken übereinstimmen.
Satz XII.1 (Kongruenzsatz sss):
Zwei Dreiecke  und
und  sind kongruent zueinander, wenn gilt:
sind kongruent zueinander, wenn gilt: 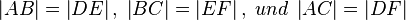 .
.
Beweis:
Neben dem Kongruenzsatz sss gibt es noch drei weitere Kongruenzsätze, die Sie aus der Schule sicherlich noch kennen. Auch diese Sätze lassen sich mit abbildungsgeometrischen Methoden beweisen. Wir werden im Rahmen dieser Veranstaltung aus Zeitgründen aber auf diese Beweise verzichten.
Formulieren Sie hier die drei noch fehlenden Kongruenzsätze:

