Diskussion Schubspiegelung: Was ist denn dann damit?
Inhaltsverzeichnis |
Folgende Applikation sei gegeben
Flo 60
Wo ist der Denkfehler oder was muss berücksichtigt werden, damit diese Konstellation nach unserer Definition auch eine Schubspiegelung ist oder brauchen wir gar eine neue Definition? --Flo60 17:27, 14. Dez. 2011 (CET)
Pipi Langsocke
Hey Flo! Ich habe mir den Fall aus der Übung vom 01.12. notiert und dort haben wir das als Verschiebung gekennzeichnet. Allerdings führt man nur die ersten beiden Verknüpfungen aus, ist es auch eine Verschiebung, danach aber eine Spiegelung. Und vorher wurde verschoben. Ich frage mich das gleiche auch gerade... Pipi Langsocke 09:54, 15. Dez. 2011 (CET)
*m.g.*
Wegen 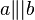 ist
ist 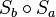 eine Verschiebung. dieselbe Verschiebung erhält man durch die NAF zweier Geradenspiegelungen an
eine Verschiebung. dieselbe Verschiebung erhält man durch die NAF zweier Geradenspiegelungen an 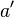 und
und 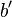 mit
mit 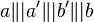 und
und 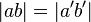 . Wählen
. Wählen 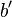 derart, dass
derart, dass 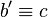 . Dann gilt
. Dann gilt 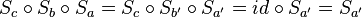 . Das Ganze ist also eine Geradenspiegelung.
Die Einschränkung in der Definition Schubspiegelung scheint Sinn zu haben.--*m.g.* 22:55, 15. Dez. 2011 (CET)
. Das Ganze ist also eine Geradenspiegelung.
Die Einschränkung in der Definition Schubspiegelung scheint Sinn zu haben.--*m.g.* 22:55, 15. Dez. 2011 (CET)

