Dodekaeder aus einem Würfel?

Dodekaeder

Ein Dodekaeder (12-Flächler) ist - wie sein Name schon vermuten lässt - ein Polyeder aus zwölf Flächen. Dabei bestehen die Flächen alle aus zueinander kongruenten regelmäßigen Fünfecken. Dodekaeder

Das 'Würfel-Dodekaeder-Problem'

Marianne Franke beschreibt in ihrer 'Didaktik der Geometrie' (Franke, Marianne (2007): Didaktik der Geometrie in der Grundschule, Spektrum Verlag, Heidelberg, S. 174) im Bereich der räumlichen Objekte folgenden Sachverhalt:

"Sie [die Kinder] können auch von der Ecke aus schneidend den Würfel [Vollmodell] in Pyramiden zerlegen. 

Schneiden sie bei einem Würfel alle Ecken ab, ensteht evtl. ein platonischer Körper (Dodekaeder). 

Die abgeschnittenen Teile sind Pyramiden."

Wir haben es bis jetzt noch nicht hinbekommen, dies nachzuweisen und gehen von einem Fehler aus - sicher sind wir uns allerdings noch nicht (auch mit Knetmasse wurde mancherorts schon hantiert).

Hat vielleicht irgendjemand eine Vermutung, wie die Ecken abgeschnitten werden müssten?

Folgender Aspekt spricht für die Dodekaeder-Theorie

• Selbst wenn sich Franke im Dodekaeder geirrt hat - ein anderer Platonischer Körper kommt erst recht nicht in Frage (Oktaeder (8-Flächler) hat zu wenige und der Ikosaeder (20-F.) hat zu viele Flächen). Allerdings wird ja der Satz beschrieben, dass "evtl. ein platonischer Körper" ensteht - kann man sich derart irren? Wir glauben nicht!

Folgende Aspekte aber sprechen gegen die Dodekaeder-Theorie

• Ein Würfel hat zunächst per Definition (man überzeuge sich davon :) ) sechs Flächen und acht Ecken - schneidet man die Ecken ab, entsteht ein 14-Flächler
• Wenn ich die Ecken abschneide, erhalte ich (zumindest als Schnittfläche) jeweils Dreiecke - und Dreiecke sind in der Regel nicht den regelmäßigen Fünfecken zuzuordnen

Folgerung

• Wer kann helfen? Haben wir/ich einen Denkfehler gemacht oder stimmt der Eintrag in Franke nicht?
• Im übrigen ist dies glaube ich auch ganz gut geeignet, mit Schülerinnen und Schüler zu diskutieren - nicht alles was in Büchern steht muss wahr sein - nur weil es in einem Buch steht. Sollte es aber wahr sein, sollte man Mittel und Wege wissen, wie man das Überprüfen kann (Stichwort: Mündiger Bürger)

ich versteh das auch nicht. sie scheint aber auch nicht zu glauben, was sie schreibt (..., entsteht evtl. ein platonischer körper.")
vielleicht meint sie was gaaanz anderes, etwas wie auf seite 4/5? [1]--Studentin 01:03, 17. Jul. 2012 (CEST)

Ach wenn ich doch nur Knete hätt'... --Flo60 22:09, 16. Jul. 2012 (CEST) ich bring dir morgen knete mit: bin von 8-14 uhr an der neuen ph, die ersten beiden stunden in der geometrievorlesung im hörsaalgebäude--Studentin 01:03, 17. Jul. 2012 (CEST)

Würfel Ecken abschneiden

Mögliche Lösung

Zunächst muss ich mich bei meiner Lieblingsgeowikikritikerin (und -monddidaktikerin :) ) entschuldigen, dass ich sie in der 'realen Welt' (also vor dem Hörsaalgebäude) am Dienstag nicht abgewartet habe und sie die Knete quasi umsonst mitgebracht hat - t'schuldige :(

Aber natürlich waren wir dabei nicht ganz untätig, sondern im Auftrag des 'Würfel-Dodekaeder-Problems' unterwegs. Und wir haben eine mögliche Lösung gefunden:
Wie auch schon im Skript zu erkennen ist, kann aus dem Würfel ein Tetraeder geschnitzt werden - wir haben dazu das passende Papiermodell begutachtet.

Was ist im Übrigen die beste Eselsbrücke für Tetraeder? Man denke einfach an die Petra Eder :-)))) --Flo60 20:57, 18. Jul. 2012 (CEST)

hier der tetraeder in stereo:






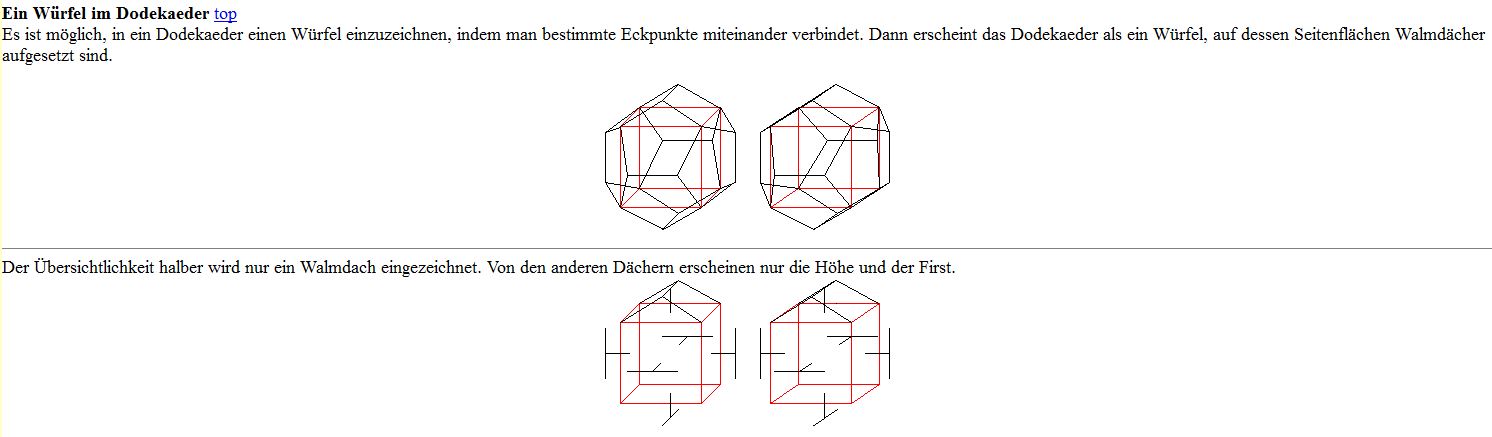
und wenn schon kein dodekaeder aus einem würfel, dann wenigstens ein würfel aus einem dodekaeder (dächer abschneiden):



--Studentin 10:05, 19. Jul. 2012 (CEST)